题目内容
已知两个二次函数：f（x）=ax2+bx+1与g（x）=a2x2+bx+1（a＞1）．若x1，x2（其中x1＜x2）是方程f（x）=0的二根；若x3，x4（若是x3＜x4）是方程g（x）=0的二根．则 x1，x2，x3，x4的大小关系是（ ）
分析：构造两个函数：F（x）=f（x）-1，G（x）=g（x）-1，通过讨论它们的零点，得出它们的根之间的大小关系．然后通过分类讨论和在同一坐标系里作出F（x）和G（x）的图象，然后将两个图象向上平移一个单位，可得x1，x2，x3，x4的大小关系，最后综合可得出正确的大小关系．
解答：解：记函数F（x）=f（x）-1=ax2+bx，G（x）=g（x）-1=a2x2+bx
两个函数有公共的零点x=0，此外F（x）还有一个零点x=-
，G（x）还有一个零点x=-
，
①因为a＞1，当b＜0时，
得必定有0＜-
＜ -
，
在同一坐标系里作出F（x）和G（x）的图象：
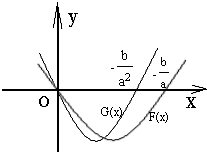
将此两个图象都上移一个单位，可得函数f（x）和g（x）的图象
所以由图象可得x1＜x3＜x4＜x2
②当b＞0时，同理可得四个根的大小关系：x1＜x3＜x4＜x2
综上所述，可判断x1，x2，x3，x4的大小关系为：x1＜x3＜x4＜x2
故选A．
两个函数有公共的零点x=0，此外F（x）还有一个零点x=-
| b |
| a |
| b |
| a2 |
①因为a＞1，当b＜0时，
得必定有0＜-
| b |
| a2 |
| b |
| a |
在同一坐标系里作出F（x）和G（x）的图象：
将此两个图象都上移一个单位，可得函数f（x）和g（x）的图象
所以由图象可得x1＜x3＜x4＜x2
②当b＞0时，同理可得四个根的大小关系：x1＜x3＜x4＜x2
综上所述，可判断x1，x2，x3，x4的大小关系为：x1＜x3＜x4＜x2
故选A．
点评：本题以一元二次方程的根的分布考查了二次函数的图象与性质，所含字母参数较多，属于难题．采用数形结合与分类讨论的思想解题，是本题解决的关键所在．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目