题目内容
已知命题p:方程a2x2+ax-2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,则a的取值范围是分析:对方程a2x2+ax-2=0进行因式分解是解决该题的关键,得出方程的根(用a表示出).利用根在[-1,1]上,得出关于a的不等式,求出命题p为真的a的范围,利用x2+2ax+2a≤0相应的二次方程的判别式等于0得出关于a的方程,求出a,再根据“p或q”是假命题得出a的范围.
解答:解:由a2x2+ax-2=0,得(ax+2)(ax-1)=0,
显然a≠0,∴x=-
,或x=
.
∵x∈[-1,1],∴|-
|≤1或|
|≤1,∴|a|≥1.
只有一个实数x满足不等式x2+2ax+2a≤0,即抛物线y=x2+2ax+2a与x轴只有一个交点,
∴△=4a2-8a=0,∴a=0或a=2.
∴命题“p或q”为真命题时,|a|≥1或a=0.
∵命题“p或q”为假命题,
∴a的取值范围为{a|-1<a<0或0<a<1}.
故答案:-1<a<0或0<a<1.
显然a≠0,∴x=-
| 2 |
| a |
| 1 |
| a |
∵x∈[-1,1],∴|-
| 2 |
| a |
| 1 |
| a |
只有一个实数x满足不等式x2+2ax+2a≤0,即抛物线y=x2+2ax+2a与x轴只有一个交点,
∴△=4a2-8a=0,∴a=0或a=2.
∴命题“p或q”为真命题时,|a|≥1或a=0.
∵命题“p或q”为假命题,
∴a的取值范围为{a|-1<a<0或0<a<1}.
故答案:-1<a<0或0<a<1.
点评:本题考查命题真假的判断,利用因式分解求出方程的根是解决本题的关键,再根据一元二次不等式与二次方程的关系转化相应的不等式问题,考查学生的等价转化思想,考查学生对复合命题真假的判断准则.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
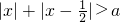 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围. 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围.