题目内容
在正方体 中,
中, 是棱
是棱 的中点,则
的中点,则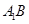 与
与 所成角的余弦值为( )
所成角的余弦值为( )
A.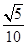 | B. | C. | D. |
B.
解析试题分析:在正方体 中,连接
中,连接 ,则∠ED1C即为异面直线
,则∠ED1C即为异面直线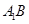 与
与 所成角。设正方体
所成角。设正方体 的边长为1,则在△ED1C中,
的边长为1,则在△ED1C中, ,
, ,EC=
,EC= ,所以由余弦定理,得:cos∠ED1C=
,所以由余弦定理,得:cos∠ED1C= 。
。
考点:本题考查异面直线所成的角和余弦定理。
点评:两异面直线所成角的范围为 ,当求得某个角的余弦值为负时,则这个角的补角才是异面直所成的角。
,当求得某个角的余弦值为负时,则这个角的补角才是异面直所成的角。

练习册系列答案
相关题目
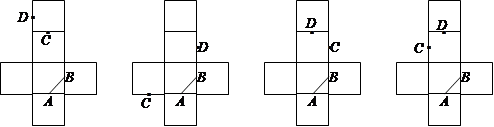
将下面的平面图形(每个点都是正三角形的顶点或边的中点)沿虚线折成一个正四面体后,直线 与
与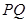 是异面直线的是( )
是异面直线的是( )
C
① ② ③ ④
| A.①② | B.②④ | C.①④ | D.①③ |
下列说法不正确的是( )
| A.空间中,一组对边平行且相等的四边形是一定是平行四边形; |
| B.过一条直线有且只有一个平面与已知平面垂直. |
| C.过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内; |
D.存在两条异面直线 ,使得 ,使得 ; ; |




 ),则该棱锥的体积是( )
),则该棱锥的体积是( )




 分别是正方体的棱的中点,那么,在原正方体中,
分别是正方体的棱的中点,那么,在原正方体中, 与
与 所在直线为异面直线的是
所在直线为异面直线的是