题目内容
经过点![]() 且与直线
且与直线![]() 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为![]() .点
.点![]() 、
、![]() 在轨迹
在轨迹![]() 上,且关于
上,且关于![]() 轴对称,过线段
轴对称,过线段![]() (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线![]() ,使直线
,使直线![]() 与轨迹
与轨迹![]() 在点
在点![]() 处的切线平行,设直线
处的切线平行,设直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)证明:![]() ;
;
(3)若点![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,且△
,且△![]() 的面积为20,求直线
的面积为20,求直线![]() 的方程。
的方程。
(1)方法1:设动圆圆心为![]() ,依题意得,
,依题意得,![]() .
.
整理,得![]() .所以轨迹
.所以轨迹![]() 的方程为
的方程为![]()
方法2:设动圆圆心为![]() ,依题意得点
,依题意得点![]() 到定点
到定点![]() 的距离和点
的距离和点![]() 到定直线
到定直线![]() 的距离相等,
的距离相等,
根据抛物线的定义可知,动点![]() 的轨迹是抛物线.
的轨迹是抛物线.
且其中定点![]() 为焦点,定直线
为焦点,定直线![]() 为准线.
为准线.
所以动圆圆心![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)由(1)得![]() ,即
,即![]() ,则
,则![]() .
.

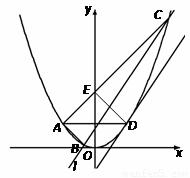 设点
设点![]() ,由导数的几何意义知,直线
,由导数的几何意义知,直线![]() 的斜率为
的斜率为![]() .
.
由题意知点![]() .设点
.设点![]() ,
,![]() ,
,
则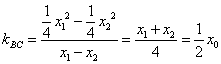 ,
,
即![]() .
.
因为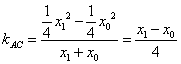 ,
,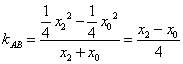 .
.
由于![]() ,即
,即![]() .
.
所以![]() .
.
(3)方法1:由点![]() 到
到![]() 的距离等于
的距离等于![]() ,可知
,可知![]()
![]() .
.
不妨设点![]() 在
在![]() 上方(如图),即
上方(如图),即![]() ,直线
,直线![]() 的方程为:
的方程为:![]() .
.
由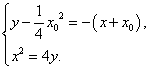
解得点![]() 的坐标为
的坐标为![]() .
.
所以![]() .
.
由(2)知![]()
![]() ,同理可得
,同理可得![]() .
.
所以△![]() 的面积
的面积![]() ,
,
解得![]() .
.
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
方法2:由点![]() 到
到![]() 的距离等于
的距离等于![]() ,可知
,可知![]()
![]() .
.
由(2)知![]()
![]() ,所以
,所以![]()
![]() ,即
,即![]() .
.
由(2)知![]() ,
,![]() .
.
所以![]() .
.
即![]() . ①
. ①
由(2)知![]() . ②
. ②
不妨设点![]() 在
在![]() 上方(如图),即
上方(如图),即![]() ,由①、②解得
,由①、②解得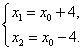
因为 ,
,
同理![]() .
.
以下同方法1.
【解析】

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
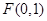 且与直线
且与直线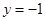 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为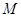 .点
.点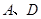 在轨迹
在轨迹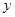 轴对称,过线段
轴对称,过线段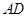 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线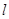 ,使直线
,使直线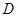 处的切线平行,设直线
处的切线平行,设直线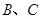 .
.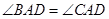 ;
;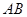 的距离等于
的距离等于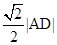 ,且
,且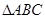 的面积为20,求直线
的面积为20,求直线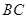 的方程.
的方程.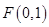 且与直线
且与直线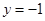 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为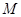 .点
.点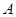 、
、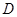 在轨迹
在轨迹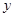 轴对称,过线段
轴对称,过线段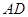 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线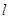 ,使直线
,使直线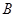 、
、 .
.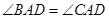 ;
;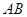 的距离等于
的距离等于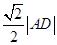 ,且△
,且△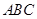 的面积为20,求直线
的面积为20,求直线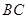 的方程.
的方程.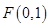 且与直线
且与直线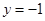 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为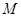 .点
.点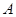 、
、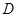 在轨迹
在轨迹 轴对称,过线段
轴对称,过线段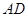 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线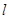 ,使直线
,使直线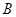 、
、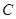 .
.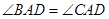 ;
;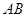 的距离等于
的距离等于 ,且△
,且△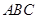 的面积为20,求直线
的面积为20,求直线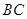 的方程.
的方程. 的导数
的导数 为实数,
为实数, .
. 且与曲线
且与曲线 的方程;
的方程; ,试判断函数
,试判断函数 的极值点个数。
的极值点个数。