题目内容
已知 是定义在
是定义在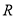 上的奇函数,当
上的奇函数,当 时,
时, .
.
(1)求 ;
;
(2)求 的解析式;
的解析式;
(3)若 ,求区间
,求区间 .
.
(1)6;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)利用奇函数的性质 进行转化计算即可;(2)因为当
进行转化计算即可;(2)因为当 时,
时, ,利用奇函数的性质先求出
,利用奇函数的性质先求出 时的解析式
时的解析式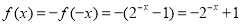 ,最后写出函数的解析式即可;(3)根据函数的单调性,求解不等式
,最后写出函数的解析式即可;(3)根据函数的单调性,求解不等式 即分别求解不等式组
即分别求解不等式组 与
与 ,最后取并集即可.
,最后取并集即可.
试题解析:(1)∵ 是奇函数
是奇函数
∴ 3分
3分
(2)设 ,则
,则 ,∴
,∴
∵ 为奇函数,∴
为奇函数,∴ 5分
5分
∴ 6分
6分
(3)根据函数图像可得 在
在 上单调递增 7分
上单调递增 7分
当 时,
时, 解得
解得 9分
9分
当 时,
时, 解得
解得 11分
11分
∴区间 为
为 12分.
12分.
考点:1.函数的奇偶性;2.函数的解析式;3.指数函数的性质.

练习册系列答案
相关题目
































