题目内容
命题P:若x,y∈R.则|x|+|y|>1是|x+y|>1的充分而不必要条件;命题q:函数y=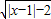 的定义域是(-∞,-1]∪[3,+∞),则( )
的定义域是(-∞,-1]∪[3,+∞),则( )A.“p或q”为假
B.“p∧q”为真
C.“p∧¬q”为真
D.“¬p∧q”为真
【答案】分析:若|x|+|y|>1,不能推出|x+y|>1,而|x+y|>1,一定有|x|+|y|>1,故命题p为假.又由函数y=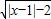 的定义域为x∈(-∞,-1]∪[3,+∞),q为真命题.
的定义域为x∈(-∞,-1]∪[3,+∞),q为真命题.
解答:解:∵|x+y|≤|x|+|y|,
若|x|+|y|>1,不能推出|x+y|>1,而|x+y|>1,一定有|x|+|y|>1,故命题p为假,¬p为 真
又由函数y=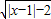 的定义域为|x-1|-2≥0,即|x-1|≥2,即x-1≥2或x-1≤-2.
的定义域为|x-1|-2≥0,即|x-1|≥2,即x-1≥2或x-1≤-2.
故有x∈(-∞,-1]∪[3,+∞).
∴q为真命题,¬q”为假
根据复合命题的真假关系可知,“p或q”为真,“p∧q”为假,“p∧¬q”为假,¬p∧q”为真
故选D.
点评:本题考查复合命题的真假,解题时要注意公式的灵活运用,熟练掌握复合命题真假的判断方法.
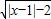 的定义域为x∈(-∞,-1]∪[3,+∞),q为真命题.
的定义域为x∈(-∞,-1]∪[3,+∞),q为真命题.解答:解:∵|x+y|≤|x|+|y|,
若|x|+|y|>1,不能推出|x+y|>1,而|x+y|>1,一定有|x|+|y|>1,故命题p为假,¬p为 真
又由函数y=
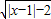 的定义域为|x-1|-2≥0,即|x-1|≥2,即x-1≥2或x-1≤-2.
的定义域为|x-1|-2≥0,即|x-1|≥2,即x-1≥2或x-1≤-2.故有x∈(-∞,-1]∪[3,+∞).
∴q为真命题,¬q”为假
根据复合命题的真假关系可知,“p或q”为真,“p∧q”为假,“p∧¬q”为假,¬p∧q”为真
故选D.
点评:本题考查复合命题的真假,解题时要注意公式的灵活运用,熟练掌握复合命题真假的判断方法.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
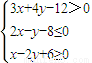 (x,y∈R),命题q:x2+y2≤r2(x,y,r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的取值范围是 .
(x,y∈R),命题q:x2+y2≤r2(x,y,r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的取值范围是 .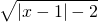 的定义域是(-∞,-1]∪[3,+∞),则
的定义域是(-∞,-1]∪[3,+∞),则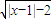 的定义域是(-∞,-1]∪[3,+∞),则( )
的定义域是(-∞,-1]∪[3,+∞),则( )