题目内容
当0<a<1时,不等式组
的解集为
|
[-1,a+2]
[-1,a+2]
.分析:把不等式组的第一个不等式左边分解因式,求出一元二次不等式的解集,再求出第二个绝对值不等式的解集,由a的范围判断端点值的大小,根据判断的结果把两解集画在数轴上,根据取解集的方法找出两解集的公共部分,即可得到原不等式组的解集.
解答:解:
,
由①变形得:(x-3)(x+1)≤0,
解得:-1≤x≤3,
由②变形得:-2≤x-a≤2,
解得:a-2≤x≤a+2,
又0<a<1,得到-2<a-2<-1,2<a+2<3,
∴a-2<-1,a+2<3,
根据题意画出相应的图形,如图所示:
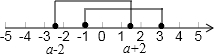
则原不等式组的解集为[-1,a+2].
故答案为:[-1,a+2]
|
由①变形得:(x-3)(x+1)≤0,
解得:-1≤x≤3,
由②变形得:-2≤x-a≤2,
解得:a-2≤x≤a+2,
又0<a<1,得到-2<a-2<-1,2<a+2<3,
∴a-2<-1,a+2<3,
根据题意画出相应的图形,如图所示:

则原不等式组的解集为[-1,a+2].
故答案为:[-1,a+2]
点评:此题考查了其他不等式的解法,利用了转化及数形结合的思想,要求学生掌握一元二次不等式及绝对值不等式的解法,会根据端点值的大小,借助数轴来解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目