题目内容
D、E、F分别是△ABC的三条边AB、BC、CA上的动点,且它们在初始时刻分别从A、B、C出发,各以一定速度沿各边向B、C、A移动.当t=1时,分别到达B、C、A.求证:在0≤t≤1的任一时刻t1,△DEF的重心不变.
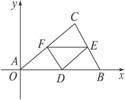
图11
证明:如图11.
建立如图所示的平面直角坐标系,设A、B、C坐标分别为(0,0),(a,0),(m,n).
在任一时刻t1∈(0,1),因速度一定,其距离之比等于时间之比,有![]() =λ,由定比分点的坐标公式可得D、E、F的坐标分别为(at1,0),(a+(m-a)t1,nt1),(m-mt1,n-nt1).由重心坐标公式可得△DEF的重心坐标为(
=λ,由定比分点的坐标公式可得D、E、F的坐标分别为(at1,0),(a+(m-a)t1,nt1),(m-mt1,n-nt1).由重心坐标公式可得△DEF的重心坐标为(![]() ).
).
当t=0或t=1时,△ABC的重心也为(![]() ),
),
故对任一t1∈[0,1],△DEF的重心不变.
点评:主要考查定比分点公式及建立平面直角坐标系,只要证△ABC的重心和时刻t1的△DEF的重心相同即可.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
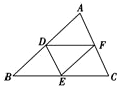 如图,D,E,F分别是△ABC的边AB,BC,CA的中点,则( )
如图,D,E,F分别是△ABC的边AB,BC,CA的中点,则( )A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,四面体PABC的六条棱均相等,D、E、F分别是AB、BC、CA的中点,则下列四个结论中不成立的是( )
如图,四面体PABC的六条棱均相等,D、E、F分别是AB、BC、CA的中点,则下列四个结论中不成立的是( )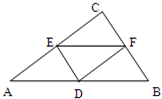 如图△ABC中,D,E,F分别是AB,AC,BC的中点,则下列各式不正确的是( )
如图△ABC中,D,E,F分别是AB,AC,BC的中点,则下列各式不正确的是( )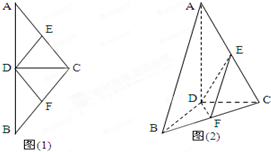 (2012•韶关二模)如图(1)在等腰△ABC中,D、E、F分别是AB、AC、BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD.(如图(2))
(2012•韶关二模)如图(1)在等腰△ABC中,D、E、F分别是AB、AC、BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD.(如图(2))