题目内容
如图, 在矩形 中,点
中,点 分别在线段
分别在线段 上,
上, .沿直线
.沿直线 将
将  翻折成
翻折成 ,使平面
,使平面 .
.
(Ⅰ)求二面角 的余弦值;
的余弦值;
(Ⅱ)点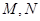 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四边形
将四边形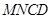 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段 的长。
的长。

【答案】
(1) ;(2)21/4.
;(2)21/4.
【解析】本试题主要是考查了立体几何中的二面角的求解以及折叠图中的线段的长度问题。
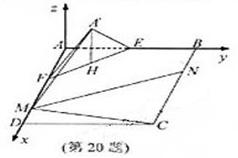
(Ⅰ)解:取线段EF的中点H,连结A’H,因为 =
= 及H是EF的中点,所以A’H
及H是EF的中点,所以A’H EF,
EF,
又因为平面A’EF 平面BEF.如图建立空间直角坐标系A-xyz,
平面BEF.如图建立空间直角坐标系A-xyz,
则A’(2,2, ),C(10,8,0),F(4,0,0),D(10,0,0).
),C(10,8,0),F(4,0,0),D(10,0,0).
故 =(-2,2,
=(-2,2, ),
), =(6,0,0).
=(6,0,0).
设 =(x,y,z)为平面A’FD的一个法向量,
=(x,y,z)为平面A’FD的一个法向量,
 -2x+2y+
-2x+2y+ z=0
z=0
所以 6x=0.
取 ,则
,则 。又平面BEF的一个法向量
。又平面BEF的一个法向量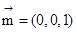 ,
,
故 。 所以二面角的余弦值为
。 所以二面角的余弦值为
(Ⅱ)解:设FM=X则M(4+X,0,0),
因为翻折后,C与A重合,所以CM=A’M,
得X=21/4,
经检验,此时点N在线段BC上,所以FM=21/4。

练习册系列答案
相关题目
 中,
中, 点
点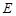 为
为 的中点,点
的中点,点 在边
在边 上,若
上,若 ,则
,则 的值是 .
的值是 .
 中,
中, 点
点 为
为 的中点,点
的中点,点 在边
在边 上,若
上,若 ,则
,则 的值是 .
的值是 .
 中,
中, 点
点 为
为 的中点,
的中点, 在边
在边 上,且
上,且 ,则
,则 的值是 .
的值是 .
 中,点
中,点 分别
分别 上,
上,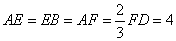 .沿直线
.沿直线
 翻折成
翻折成 ,使平面
,使平面 .
.
 的余弦值;
的余弦值; 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四
将四 向上翻折,使
向上翻折,使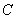 与
与 重合,求线段
重合,求线段