题目内容
设复数z=1+i,若z,
对应的向量分别为
和
,则|
|的值为
.
| 1 |
| z |
| OA |
| OB |
| AB |
| ||
| 2 |
| ||
| 2 |
分析:由已知中复数z=1+i,若z,
对应的向量分别为
和
,我们可以分别求出向量
和
的坐标,进而根据向量减法的三角形法则,求出向量
的坐标,代入向量模的计算公式,即可得到|
|的值.
| 1 |
| z |
| OA |
| OB |
| OA |
| OB |
| AB |
| AB |
解答:解:∵复数z=1+i,
∴
=
-
i
则
=(1,1),
=(
,-
)
∴|
|=|
-
|=|(-
,-
)|=
=
故答案为:
∴
| 1 |
| z |
| 1 |
| 2 |
| 1 |
| 2 |
则
| OA |
| OB |
| 1 |
| 2 |
| 1 |
| 2 |
∴|
| AB |
| OB |
| OA |
| 1 |
| 2 |
| 3 |
| 2 |
(-
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查的知识点是复数的代数表示法及其几何意义,向量减法的三角形法则,向量的模,其中根据已知条件,求出向量
的坐标,是解答本题的关键.
| AB |

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 对应的向量分别为
对应的向量分别为 和
和 ,则|
,则| |的值为________.
|的值为________.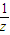 对应的向量分别为
对应的向量分别为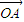 和
和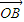 ,则|
,则|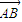 |的值为 .
|的值为 .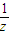 对应的向量分别为
对应的向量分别为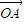 和
和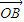 ,则|
,则|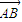 |的值为 .
|的值为 .