题目内容
数关于x的函数f(x)=sin(x+φ)有以下命题:
①?φ∈R,f(x+2π)=f(x);
②?φ∈R,f(x+1)=f(x);
③?φ∈R,f(x)都不是偶函数;
④?φ∈R,使f(x)是奇函数.
其中假命题的序号是
①?φ∈R,f(x+2π)=f(x);
②?φ∈R,f(x+1)=f(x);
③?φ∈R,f(x)都不是偶函数;
④?φ∈R,使f(x)是奇函数.
其中假命题的序号是
②③
②③
.分析:由题意确定φ的值,分析函数的周期性及奇偶性,逐一比照四个命题,判断它们的真假,得到答案即可.
解答:解:∵f(x)=sin(x+φ)的周期为2π,故?φ∈R,f(x+2π)=f(x),即①正确,②错误
当φ=2kπ,k∈Z时,f(x)=sinx是奇函数.
当φ=2(k+1)π,k∈Z时f(x)=-sinx仍是奇函数.
当φ=2kπ+
,k∈Z时,f(x)=cosx或当φ=2kπ-
,k∈Z时,f(x)=-cosx,f(x)都是偶函数.
故③错误;④正确;
故假命题的序号是:②③
故答案为:②③
当φ=2kπ,k∈Z时,f(x)=sinx是奇函数.
当φ=2(k+1)π,k∈Z时f(x)=-sinx仍是奇函数.
当φ=2kπ+
| π |
| 2 |
| π |
| 2 |
故③错误;④正确;
故假命题的序号是:②③
故答案为:②③
点评:本题以命题的真假判断为载体考查了三角函数的奇偶性和周期性,熟练掌握三角函数的图象和性质是解答的关键.

练习册系列答案
相关题目
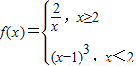 若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是 .
若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是 .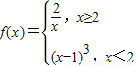 若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是 .
若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是 .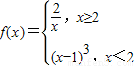 若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是 .
若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是 .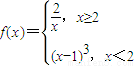 若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是 .
若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是 .