题目内容
函数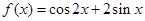 的最小值和最大值分别为( )
的最小值和最大值分别为( )
A.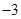 、 、 | B.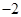 、 、 | C.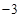 、 、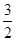 | D.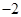 、 、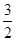 |
C
解析试题分析: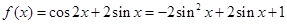
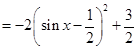 ,又
,又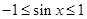 ,当
,当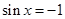 时,
时,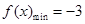 ,当
,当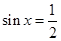 时,
时,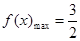 ,故选择C.三角函数最值的研究,主要有两个去向:一是转化为
,故选择C.三角函数最值的研究,主要有两个去向:一是转化为 型;二是转化为
型;二是转化为 型,但是都必须注意正、余弦函数自身的有界性,否则易犯错.
型,但是都必须注意正、余弦函数自身的有界性,否则易犯错.
考点:三角函数与二次函数的综合.

练习册系列答案
相关题目
下列命题正确的个数是
①命题“  ”的否定是“
”的否定是“  ”:
”:
②函数  的最小正周期为“
的最小正周期为“  ”是“a=1”的必要不充分条件;
”是“a=1”的必要不充分条件;
③ 在
在  上恒成立
上恒成立
 在
在  上恒成立;
上恒成立;
④“平面向量  与
与  的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“  ”
”
| A.1 | B.2 | C.3 | D.4 |
已知角 的终边上有一点P
的终边上有一点P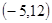 ,则
,则 的值是( ).
的值是( ).
A. | B. | C. | D. |
 是第( )象限角.
是第( )象限角.
| A.一 | B.二 | C.三 | D.四 |
sin480°等于( ).
A.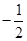 | B. | C. | D. |
函数 ,
,
 的图象与
的图象与 轴交于
轴交于 点,过点
点,过点 的直线
的直线 与函数的图象交于
与函数的图象交于 两点,则
两点,则
 ( )
( )
| A.4 | B.8 | C.16 | D.32 |
要得到函数y= cosx的图象,只需将函数y=
cosx的图象,只需将函数y= sin(2x+
sin(2x+ )的图象上所有的点的( ).
)的图象上所有的点的( ).
A.横坐标缩短到原来的 倍(纵坐标不变),再向左平行移动 倍(纵坐标不变),再向左平行移动 个单位长度 个单位长度 |
B.横坐标缩短到原来的 倍(纵坐标不变),再向右平行移动 倍(纵坐标不变),再向右平行移动 个单位长度 个单位长度 |
C.横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动 个单位长度 个单位长度 |
D.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动 个单位长度 个单位长度 |
已知函数 是定义在
是定义在 上的偶函数,且在区间
上的偶函数,且在区间 上是增函数.令
上是增函数.令 ,
, ,
, ,则( )
,则( )
A. | B. | C. | D. |
已知函数 ,其中
,其中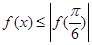 对
对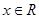 恒成立,且
恒成立,且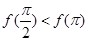 ,则
,则 的单调递增区间是( )
的单调递增区间是( )
A.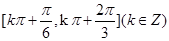 |
B.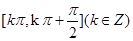 |
C.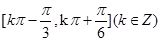 |
D.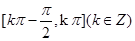 |