题目内容
3.已知向量$\overrightarrow{a}$=(-2,1),$\overrightarrow{b}$=(3,-4)且$\overrightarrow{a}$•$\overrightarrow{c}$=-1,$\overrightarrow{b}$•$\overrightarrow{c}$=9,则$\overrightarrow{c}$的坐标为( )| A. | (-1,-3) | B. | (-1,3) | C. | (1,3) | D. | (1,-3) |
分析 可设$\overrightarrow{c}=(x,y)$,从而根据条件进行数量积的坐标运算便可得到$\left\{\begin{array}{l}{-2x+y=-1}\\{3x-4y=9}\end{array}\right.$,解出x,y便可得出$\overrightarrow{c}$的坐标.
解答 解:设$\overrightarrow{c}=(x,y)$,则:
$\left\{\begin{array}{l}{\overrightarrow{a}•\overrightarrow{c}=-2x+y=-1}\\{\overrightarrow{b}•\overrightarrow{c}=3x-4y=9}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$;
∴$\overrightarrow{c}=(-1,-3)$.
故选:A.
点评 考查向量坐标的概念,以及向量数量积的坐标运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
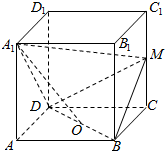 如图,在正方体ABCD-A1B1C1D1中,M为CC1的中点.
如图,在正方体ABCD-A1B1C1D1中,M为CC1的中点.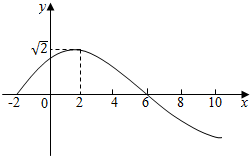 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0.|φ|<$\frac{π}{2}$)的部分函数图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0.|φ|<$\frac{π}{2}$)的部分函数图象如图所示.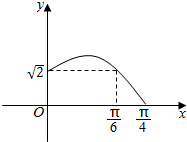 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.