题目内容
已知点A （x1，y1）；B（x2，y2）是定义在区间M上的函数y=f（x）的图象任意不重合两点，直线AB的斜率总小于零，则函数y=f（x） 在区间M上总是（ ）
分析：由点A、B不重合，不妨设x1＜x2，则x1-x2＜0，由斜率小于0可得f（x1）和f（x2）的大小关系，结合单调性的定义可得结论．
解答：解：∵点A、B在函数y=f（x）的图象上，
∴y1=f（x1），y2=f（x2），
由点A、B不重合，不妨设x1＜x2，则x1-x2＜0，
∵直线AB的斜率总小于零，
∴
=
＜0，
∵x1-x2＜0，
∴f（x1）-f（x2）＞0，
即f（x1）＞f（x2），
∴f（x）在在M上减函数，
故选C．
∴y1=f（x1），y2=f（x2），
由点A、B不重合，不妨设x1＜x2，则x1-x2＜0，
∵直线AB的斜率总小于零，
∴
| y1-y2 |
| x1-x2 |
| f(x1)-f(x2) |
| x1-x2 |
∵x1-x2＜0，
∴f（x1）-f（x2）＞0，
即f（x1）＞f（x2），
∴f（x）在在M上减函数，
故选C．
点评：本题考查函数单调性的判断、直线的斜率公式，定义是判断函数单调性的基本方法，要熟练掌握．
练习册系列答案
相关题目
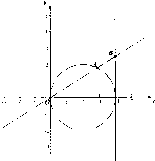已知点A（x1，y1）在圆（x-2）2+y2=4上运动，点A不与（0，0）重合，点B（4，y0）在直线x=4上运动，动点M（x，y）满足