题目内容
某工厂2010年第三季度生产的A,B,C,D四种型号的产品产量用条形图形表示如图,现用分层抽样的方法从中选取50件样品参加2011年4月份的一个展销会。

(1)A,B,C,D型号的产品各抽取多少件?
(2)从50件样品随机地抽取2件,求这2件产品恰好是不同型号产品的概率。
(3)从A,C型号的样品中随机地抽取3件,用ξ表示抽取A型号的产品件数,求ξ的分布列和数学期望

(1)A,B,C,D型号的产品各抽取多少件?
(2)从50件样品随机地抽取2件,求这2件产品恰好是不同型号产品的概率。
(3)从A,C型号的样品中随机地抽取3件,用ξ表示抽取A型号的产品件数,求ξ的分布列和数学期望
解:(1)从条形图上可知,共生产产品有50+100+150+200=500(件)
样品比为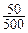 =
=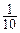 ,
,
所以A,B,C,D四种型号的产品分别取
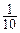 ×100=10,
×100=10,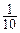 ×200=20,
×200=20,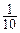 ×50=5,
×50=5,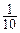 ×150=15,
×150=15,
即样本中应抽取A产品10件,B产品20件,C产品5件,D产品15件……4分
(2)从50件产品中任取2件共有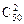 =1225种方法,
=1225种方法,
2件恰为同一产品的方法为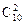 +
+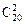 +
+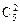 +
+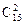 =350种,
=350种,
所以2件恰好为不同型号的产品的概率为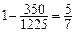 ………………………8分
………………………8分
(3)P(ξ=0)=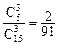 , P(ξ=1)=
, P(ξ=1)=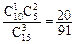 ,
,
P(ξ=2)=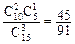 ,P(ξ=3)=
,P(ξ=3)=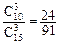 ,
,
所以ξ的分布列为
Eξ=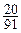 +2×
+2×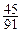 +3×
+3×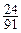 =2………………………………………12分
=2………………………………………12分
样品比为
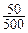 =
=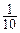 ,
,所以A,B,C,D四种型号的产品分别取
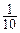 ×100=10,
×100=10,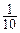 ×200=20,
×200=20,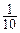 ×50=5,
×50=5,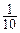 ×150=15,
×150=15,即样本中应抽取A产品10件,B产品20件,C产品5件,D产品15件……4分
(2)从50件产品中任取2件共有
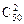 =1225种方法,
=1225种方法,2件恰为同一产品的方法为
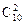 +
+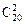 +
+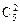 +
+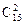 =350种,
=350种,所以2件恰好为不同型号的产品的概率为
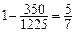 ………………………8分
………………………8分(3)P(ξ=0)=
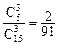 , P(ξ=1)=
, P(ξ=1)=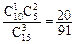 ,
,P(ξ=2)=
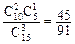 ,P(ξ=3)=
,P(ξ=3)=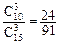 ,
,所以ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | 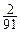 | 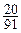 | 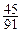 | 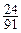 |
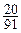 +2×
+2×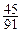 +3×
+3×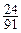 =2………………………………………12分
=2………………………………………12分略

练习册系列答案
相关题目
 的方差为
的方差为 ,则数据
,则数据 ,
, ,
, ,…,
,…, 的标准差为 ( )
的标准差为 ( )



 ,
, …
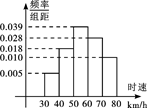
… 后画出如下频率
后画出如下频率 分布直方图.观察图形的信息,回答下列问题:
分布直方图.观察图形的信息,回答下列问题:

 ,
,
 ,
,

 个小长方形的面积和的
个小长方形的面积和的 ,且样本容量为100,则中间一组的频数为( )
,且样本容量为100,则中间一组的频数为( )