题目内容
设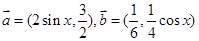 ,且
,且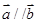 ,则锐角
,则锐角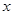 为( )
为( )
A.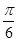 | B.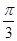 | C.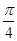 | D.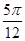 |
C.
解析试题分析:因为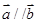 .所以
.所以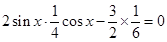 .即
.即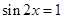 .又因为
.又因为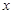 为锐角.所以
为锐角.所以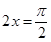 .所以
.所以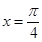 .本题主要考察向量的平行知识,通过向量平行的坐标公式来求解.本提较基础.
.本题主要考察向量的平行知识,通过向量平行的坐标公式来求解.本提较基础.
考点:1.向量平行的坐标形式.2.三角函数的知识.

练习册系列答案
相关题目
若向量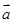 、
、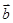 满足
满足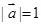 、
、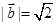 ,
,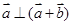 ,则
,则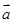 与
与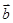 的夹角为( )
的夹角为( )
A. | B.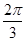 | C.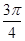 | D.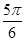 |
在平面直角坐标系中,已知向量 若
若 ,则x=( )
,则x=( )
| A.-2 | B.-4 | C.-3 | D.-1 |
设向量 =(sinα,
=(sinα, )的模为
)的模为 ,则cos2α=( )
,则cos2α=( )
A. | B. | C.﹣ | D.﹣ |
已知点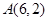 ,
,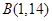 ,则与
,则与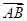 共线的单位向量为( )
共线的单位向量为( )
A.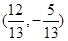 或 或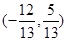 | B. |
C.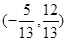 或 或 | D.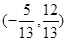 |
已知向量 满足
满足 ,且
,且 ,则
,则 在
在 方向上的投影为( )
方向上的投影为( )
| A.3 | B. . . | C. | D. |
已知 为等边三角形,
为等边三角形,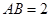 ,设
,设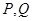 满足
满足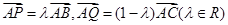 ,若
,若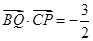 ,则
,则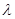 等于( )
等于( )
A.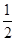 | B.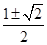 | C.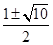 | D.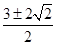 |
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量α=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为 ( )
A. | B. | C. | D. |
设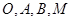 为平面上四点,
为平面上四点,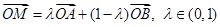 ,则
,则
A.点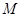 在线段 在线段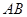 上 上 | B.点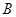 在线段 在线段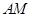 上 上 |
C.点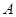 在线段 在线段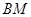 上 上 | D.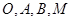 四点共线 四点共线 |