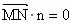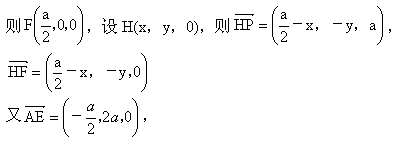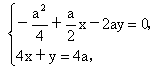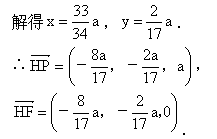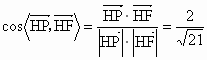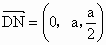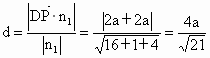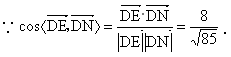题目内容
(2006
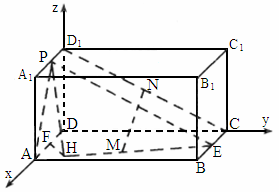
四川,19)如下图,在长方体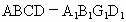 中,E、P分别是BC、
中,E、P分别是BC、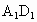 的中点,M、N分别是AE、
的中点,M、N分别是AE、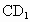 的中点,
的中点,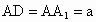 ,AB=2a.
,AB=2a.
(1)
求证:MN∥面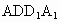 ;
;
(2)
求二面角P-AE-D的大小:(3)
求三棱锥P-DEN的体积.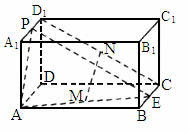
答案:略
解析:
解析:
|
解析:以 D为原点,DA、DC、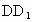 所在的直线分别为x轴、y轴、z轴,建立直角坐标系. 所在的直线分别为x轴、y轴、z轴,建立直角坐标系.
则 A(a,0,0),B(a,2a,0),C(0,2a,0),
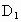 (0,0,a). (0,0,a).
∵ E、P、M、N分别是BC、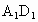 、AE、 、AE、 、的中点, 、的中点,
n=(0,1,0),显然n⊥面
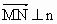 . .
又 MN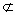 面 面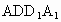 ,∴MN∥ ,∴MN∥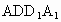 . .
(2) 过P作PH⊥AE,交AE于H.取AD的中点F,
由 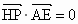 ,及H在直线AE上,可得 ,及H在直线AE上,可得
∴ 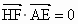 .即 .即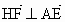 . .
∴ 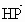 与 与 所夹的角等于二面角P-AE-D的大小. 所夹的角等于二面角P-AE-D的大小.
故二面角 P-AE-D的大小等于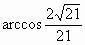 . .
(3) 设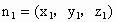 为平面DEN的法向量,则 为平面DEN的法向量,则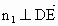 , ,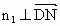 . .
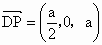 . .
∴ 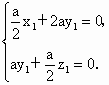 即 即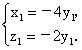
∴可取 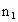 =(4,-1,2). =(4,-1,2).
∴ 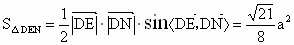 . .
∴ 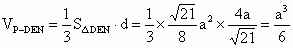 . . |

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
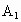 (a
(a
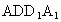 ,
,