题目内容
袋中有大小、形状相同的白、黑球各一个,现依次有放回地随机摸取3次,每次摸取一个球, 若摸到白球时得2分,摸到黑球时得1分,则3次摸球所得总分为4的概率是( )
A. | B. | C.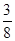 | D. |
C
解析试题分析:由于袋中有大小、形状相同的白、黑球各一个,那么每次摸到白球的概率为 ,摸到黑球的概率为
,摸到黑球的概率为 ,那么三次摸球得分为4=2+1+1,说明了一次摸到白球,两次摸到黑球,则根据独立重复试验的概率公式可知
,那么三次摸球得分为4=2+1+1,说明了一次摸到白球,两次摸到黑球,则根据独立重复试验的概率公式可知 ,选C.
,选C.
考点:本试题主要考查了独立事件的概率的求解运用。
点评:解决该试题的关键是理解有放回的抽样就是独立事件的背景,那么每次摸球互不影响。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
设随机变量X~N(0,1),已知 ,则
,则 ( )
( )
| A.0.025 | B.0.050 |
| C.0.950 | D.0.975 |
已知 是
是 所在平面内一点,
所在平面内一点, ,现将一粒
,现将一粒
黄豆随机撒在 内,则黄豆落在
内,则黄豆落在 内的概率是( )
内的概率是( )
A. | B. | C. | D. |
先后抛掷两颗骰子,设出现的点数之和是10,11,12的概率依次是P1,P2,P3,则( )
| A.P1>P2>P3 | B.P1>P2=P3 | C.P1=P2>P3 | D.P1=P2<P3 |
连掷两次骰子分别得到的点数为m和n,记向量 与向量
与向量 的夹角为
的夹角为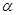 ,则
,则 的概率是( )
的概率是( )
A. | B. | C. | D. |
在商场付款处排队等候付款的人数及其概率如下:
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
A.0.9 B. 0.74 C. 0.56 D.0.26