题目内容
已知函数 满足
满足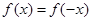 ,且当
,且当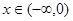 时,
时,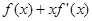
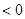 成立, 若
成立, 若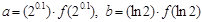 ,
, 的大小关系是( )
的大小关系是( )
A.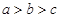 | B.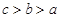 | C.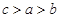 | D.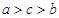 |
B
解析试题分析:构造函数g(x)=xf(x),则g'(x)=f(x)+xf′(x),
∵?x∈R不等式:f(x)+xf′(x)<0恒成立,∴g'(x)<0,即g(x)在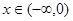 单调递减.
单调递减.
又∵函数y=f(x)满足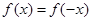 ,是定义在实数集R上的偶函数,
,是定义在实数集R上的偶函数,
∴g(x)=xf(x)是定义在实数集R上的奇函数,
∴函数g(x)在实数集R上为减函数,所以

 =
=  ,
,
-3<  <
< ,所以c>b>a,故选B.
,所以c>b>a,故选B.
考点:函数值的大小比较; 函数的单调性和导数之间的关系;导数的运算.

练习册系列答案
相关题目
函数f(x)=2x+x3-2在区间(0,1)内的零点个数是( )
| A.0 | B.1 | C.2 | D.3 |
函数 的单调递增区间是
的单调递增区间是
A. | B. | C.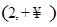 | D. |
已知函数 是
是 上的增函数,
上的增函数, 是其图像上的两点,那么
是其图像上的两点,那么 的解集为( )
的解集为( )
A. | B. | C.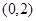 | D.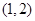 |
方程lnx=6-2x的根必定属于区间( )
| A.(-2,1) | B.(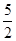 ,4) ,4) | C.(1,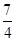 ) ) | D.(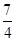 , ,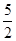 ) ) |
函数f(x)=lnx-x-a有两个不同的零点,则实数a的取值范围是( )
| A.(-∞,-1] | B.(-∞,-1) |
| C.[-1,+∞) | D.(-1,+∞) |
已知函数f(x)的图象如图所示,则f(x)的解析式可以是( )
A.f(x)= |
B.f(x)= |
C.f(x)=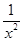 -1 -1 |
D.f(x)=x- |
已知函数g(x)=1-2x,f[g(x)]= (x≠0),则f(
(x≠0),则f( )等于( )
)等于( )
| A.1 | B.3 | C.15 | D.30 |
[2014·武汉模拟]函数f(x)= 的值域为( )
的值域为( )
| A.(-∞,-1) |
| B.(-1,0)∪(0,+∞) |
| C.(-1,+∞) |
| D.(-∞,-1)∪(0,+∞) |