题目内容
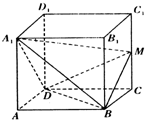 如图,在棱长为l的正方体ABCD-A1B1C1D1中,M为CC1中点.
如图,在棱长为l的正方体ABCD-A1B1C1D1中,M为CC1中点.(1)求二面角A1-BD-M的大小;
(2)求四面体A1-BDM的体积?
分析:(1)在正方体ABCD-A1B1C1D1中,棱长为l,取BD中点为O,连接OM,OA1.
说明∠A1OM为=两角A1-BD-M的平面角,在△A1OM中,由勾股定理求出二面角A1-BD-M的大小;
(2)由(1)可知A1O⊥面BDM,直接求出四面体A1-BDM体积.
说明∠A1OM为=两角A1-BD-M的平面角,在△A1OM中,由勾股定理求出二面角A1-BD-M的大小;
(2)由(1)可知A1O⊥面BDM,直接求出四面体A1-BDM体积.
解答: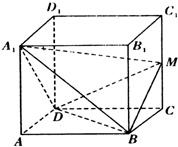 解:(1)在正方体ABCD-A1B1C1D1中,棱长为l,取BD中点为O,连接OM,OA1.
解:(1)在正方体ABCD-A1B1C1D1中,棱长为l,取BD中点为O,连接OM,OA1.
∵BM=DM=
,A1B=A1D=
从而A1O⊥BD,MO⊥BD
∴∠A1OM为=两角A1-BD-M的平面角
在△A1OM中,OM=
=
,A1O=
=
而A1M=
=
从而由勾股定理可知:∠A1OM=90°(6分)
(2)由(1)可知A1O⊥面BDM,从而四面体A1-BDM体积
V=
•S△BDM•A1O=
(
•
•
)•
=
(12分)
 解:(1)在正方体ABCD-A1B1C1D1中,棱长为l,取BD中点为O,连接OM,OA1.
解:(1)在正方体ABCD-A1B1C1D1中,棱长为l,取BD中点为O,连接OM,OA1.∵BM=DM=
| ||
| 2 |
| 2 |
从而A1O⊥BD,MO⊥BD
∴∠A1OM为=两角A1-BD-M的平面角
在△A1OM中,OM=
| BM2-OB2 |
| ||
| 2 |
| A1B2-OB2 |
| ||
| 2 |
而A1M=
A1
|
| 3 |
| 2 |
从而由勾股定理可知:∠A1OM=90°(6分)
(2)由(1)可知A1O⊥面BDM,从而四面体A1-BDM体积
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
点评:本题是中档题,考查二面角的求法,几何体的体积的求法,考查计算能力,转化思想的应用,找出二面角的平面角是解题的关键.

练习册系列答案
相关题目
 (2012•温州一模)如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( )
(2012•温州一模)如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( )


