题目内容
已知在△ABC中,sinA+cosA=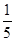 .
.
(1)求sinA·cosA;
(2)判断△ABC是锐角三角形还是钝角三角形;
(3)求tanA的值.
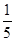 .
.(1)求sinA·cosA;
(2)判断△ABC是锐角三角形还是钝角三角形;
(3)求tanA的值.
(1)-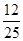 (2)钝角三角形.(3)-
(2)钝角三角形.(3)-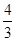
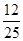 (2)钝角三角形.(3)-
(2)钝角三角形.(3)-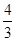
(1)因为sinA+cosA=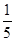 ①,两边平方得1+2sinAcosA=
①,两边平方得1+2sinAcosA=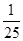 ,所以sinA·cosA=-
,所以sinA·cosA=-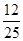 .
.
(2)由(1)sinAcosA=-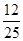 <0,且0<A<π,可知cosA<0,所以A为钝角,所以△ABC是钝角三角形.
<0,且0<A<π,可知cosA<0,所以A为钝角,所以△ABC是钝角三角形.
(3)(sinA-cosA)2=1-2sinAcosA=1+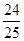 =
= .
.
又sinA>0,cosA<0,sinA-cosA>0,所以sinA-cosA=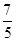 ②,
②,
所以由①,②可得sinA=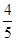 ,cosA=-
,cosA=-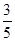 ,则tanA=
,则tanA=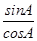 =
=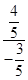 =-
=-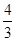 .
.
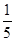 ①,两边平方得1+2sinAcosA=
①,两边平方得1+2sinAcosA=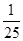 ,所以sinA·cosA=-
,所以sinA·cosA=-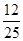 .
.(2)由(1)sinAcosA=-
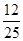 <0,且0<A<π,可知cosA<0,所以A为钝角,所以△ABC是钝角三角形.
<0,且0<A<π,可知cosA<0,所以A为钝角,所以△ABC是钝角三角形.(3)(sinA-cosA)2=1-2sinAcosA=1+
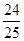 =
= .
.又sinA>0,cosA<0,sinA-cosA>0,所以sinA-cosA=
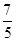 ②,
②,所以由①,②可得sinA=
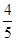 ,cosA=-
,cosA=-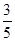 ,则tanA=
,则tanA=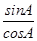 =
=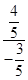 =-
=-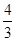 .
.
练习册系列答案
相关题目
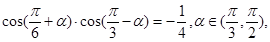 求:
求: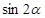 ;
;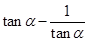 .
.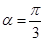 ”是“
”是“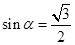 ”的( )
”的( ) ,则
,则 =
= 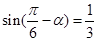 ,则
,则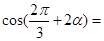 ( )
( )



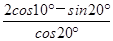 =________.
=________.  =
= ,那么cosα=________.
,那么cosα=________.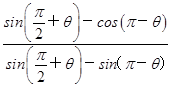 =__________.
=__________.