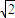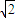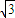Question

设长方体的对角线的长度是4，过每一顶点有两条棱与对角线的夹角都是60°，则此长方体的体积是（　　）

• A．

  3

  9

• B．8

  2

• C．8

  3

• D．16

  3

Answer 1

分析：由题意作出图形，利用解直角三角形的知识求出长方体的过一个顶点的三条棱长，从而求出长方体的体积．

解答：解：如图，

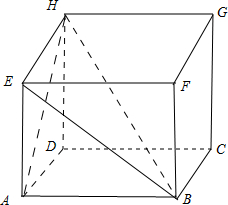
由题意可知：与对角线BH成60°角的一条棱AB和对角线所在的直角三角形中，和棱AB所对的角∠AHB是30°，可得棱AB的长度为2，
同理EH的长度也为2，在直角三角形HAB中，由勾股定理可得AH=

42-22

=2

3

，
又在直角三角形中HEA中，EA=

(2 3 )2-22

=2

2

．
所以，长方体的体积是V=2×2×2

2

=8

2

．
故选B．

点评：本小题主要考查几何体的体积，考查数形结合的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，属中档题．