题目内容
己知x>0,由不等式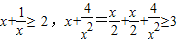 ,启发我们可以推广结论:
,启发我们可以推广结论: ,则m= .
,则m= .
【答案】分析:先根据题条件:“由不等式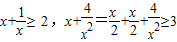 ,”启发我们可以对
,”启发我们可以对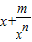 进行配凑:
进行配凑: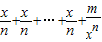 ,再利用基本不等式得得出答案.
,再利用基本不等式得得出答案.
解答:解:由不等式 ,
,
启发我们可以对 进行配凑:
进行配凑:

再利用基本不等式得:
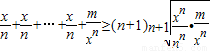 ,
,
当m=nn时,
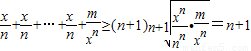 .
.
故答案为:nn
点评:本题主要考查不等式的推广、运用归纳进行推理的能力.解题的关键是理解归纳推理的意义,掌握归纳推理的方法.
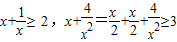 ,”启发我们可以对
,”启发我们可以对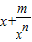 进行配凑:
进行配凑: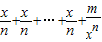 ,再利用基本不等式得得出答案.
,再利用基本不等式得得出答案.解答:解:由不等式
 ,
,启发我们可以对
 进行配凑:
进行配凑:
再利用基本不等式得:
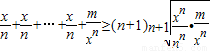 ,
,当m=nn时,
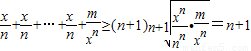 .
.故答案为:nn
点评:本题主要考查不等式的推广、运用归纳进行推理的能力.解题的关键是理解归纳推理的意义,掌握归纳推理的方法.

练习册系列答案
相关题目
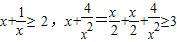 ,启发我们可以推广结论:
,启发我们可以推广结论: ,则m= .
,则m= .