题目内容
( 12分)已知集合M={-1,0,1,2},从集合M中有放回地任取两元素作为点P的坐标。
(1)( 4分)写出这个试验的所 有基本事件,并求出基本事件的个数;
有基本事件,并求出基本事件的个数;
(2)( 4分)求点P落在坐标轴上的概率;
(3)( 4分)求点P落在圆 内的概率.
内的概率.
解:(1)“从M中有放回地任取两元素作为P点的坐标”其一切可能的结果所组成的基本事件为(-1,-l),(-1,0),(-1,1),(-1,2),(0,-l),(0, 0),(0,1),(0,2),(1,
0),(0,1),(0,2),(1,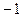 ),(1,0),(1,1),(1,2),(2,-1)(2
),(1,0),(1,1),(1,2),(2,-1)(2 ,0),(2,1),(2,2), ………………………………………………3分
,0),(2,1),(2,2), ………………………………………………3分
共有16个基 本事件组成. …………………………………………………………4分
本事件组成. …………………………………………………………4分
(2)用事件A表示“点P在坐标轴上”这一事件,……………………………………… 5分
5分
则A={(-1,0),(0,-l),(0,0),(0,1),(0,2),(1,0),(2,0)},事件A由7个基本事件组成, …………………………………………………………6分
因而P(A)=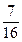 …………………………………………………………7分
…………………………………………………………7分
所以点P落在坐标轴上的概率为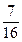 …………………………………………………8分
…………………………………………………8分
(3)用事件B 表示“点P在圆
表示“点P在圆 内”这一事件,………………………………9分
内”这一事件,………………………………9分
则B={(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1)},
事件B由9个基本事件组成, ………………………………………………………10分
因而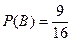 ………………………………………………………11分
………………………………………………………11分
点P落在圆 内的概率为
内的概率为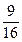 …………………………………………………12分
…………………………………………………12分
解析

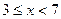 }, B={
}, B={ }, C={
}, C={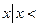 a}
a} (2)求
(2)求 ; (3)若
; (3)若 ,求a的取值范围.
,求a的取值范围. ,
, ,若
,若 ,求实数a的取值范围。
,求实数a的取值范围。
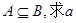 的取值范围;
的取值范围; 的值。
的值。 ,
,
 时,求
时,求
 的实数
的实数 的取值范围。
的取值范围。

 求a的取值范围.
求a的取值范围.