题目内容
若函数f(x)是定义在R上的偶函数,且对任意x∈R,总有f(x+2)=-f(x)成立,则f(19)等于( )
| A.0 | B.1 | C.18 | D.19 |
A
解析

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知f(x)是以2为周期的偶函数,且当x∈(0,1)时,f(x)=2x,则f(- )的值为( )
)的值为( )
A. | B. | C.2 | D.1 |
若关于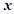 的方程
的方程 有四个不同的实数解,则实数
有四个不同的实数解,则实数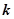 的取值范围为( )
的取值范围为( )
| A.(0,1) | B.(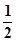 ,1) ,1) | C.(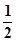 ,+∞) ,+∞) | D.(1,+∞) |
设 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则
A. | B.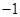 | C.1 | D.3 |
已知定义域为R的函数f(x)满足f(-x)= -f(x+4),当x>2时,f(x)单调递增,如果x1+x2<4且(x1-2)(x2-2)<0,则f(x1)+f(x2)的值( )
| A.恒小于0 | B.恒大于0 | C.可能为0 | D.可正可负 |
规定 若函数
若函数 的图象关于直线
的图象关于直线 对称,则
对称,则 的值为( )
的值为( )
| A.-2 | B.2 | C.-1 | D.1 |
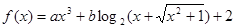 在
在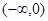 上有最小值-5,(
上有最小值-5,( ,
,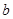 为常数),则函数
为常数),则函数 在
在 上( )
上( ) .有最大值5
.有最大值5  .有最小值5
.有最小值5 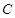 .有最大值3
.有最大值3 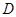 .有最大值9
.有最大值9  的图象如右图,则函数
的图象如右图,则函数 的图象为( )
的图象为( )

 的那一个图是( )
的那一个图是( )