题目内容
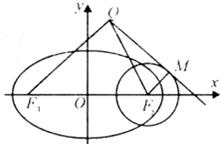 设F1,F2为椭圆C:
设F1,F2为椭圆C:| x2 |
| 6m2 |
| y2 |
| 2m2 |
| PF1 |
| PF2 |
| PF1 |
| PF2 |
(2)作以F2为圆心,以1为半径的圆,过动点Q作圆F2的切线,切点为且使|
| QF1 |
| 2 |
| QM |
分析:(1)由a2=6m2,b2=2m2,知2c2=4m2,由
•
=0,知|PF1|2+|PF2|2=(2c)2=16m2,由椭圆定义知|
| +|
| =2
m,由此能得到所求的椭圆方程.
(2)由F1(-2,0),F2(2,0),设Q(x,y),知|
| =
|
|,(x+2)2+y2=2[(x-2)2+y2-1],由此能得到所求的轨迹方程.
| PF1 |
| PF2 |
| PF1 |
| PF2 |
| 6 |
(2)由F1(-2,0),F2(2,0),设Q(x,y),知|
| QF1 |
| 2 |
| QM |
解答:解:(1)∵a2=6m2,b2=2m2,
∴2c2=4m2,
∵
•
=0,
∴|PF1|2+|PF2|2=(2c)2=16m2,
由椭圆定义知,|
| +|
| =2
m,
∴16m2+8=24m2,
∴m2=1,
故所求的椭圆方程为
+
=1.
(2)由(1)知F1(-2,0),F2(2,0),设Q(x,y),
∵|
| =
|
|,
∴|
|2=2|
|2=2(|
|2-1),
∴(x+2)2+y2=2[(x-2)2+y2-1],
化简,得(x-6)2+y2=34,
故所求的轨迹方程为(x-6)2+y2=34.
∴2c2=4m2,
∵

| PF1 |
| PF2 |
∴|PF1|2+|PF2|2=(2c)2=16m2,
由椭圆定义知,|
| PF1 |
| PF2 |
| 6 |
∴16m2+8=24m2,
∴m2=1,
故所求的椭圆方程为
| x2 |
| 6 |
| y2 |
| 2 |
(2)由(1)知F1(-2,0),F2(2,0),设Q(x,y),
∵|
| QF1 |
| 2 |
| QM |
∴|
| QF1 |
| QM |
| QF2 |
∴(x+2)2+y2=2[(x-2)2+y2-1],
化简,得(x-6)2+y2=34,
故所求的轨迹方程为(x-6)2+y2=34.
点评:本题考查椭圆的方程和点的轨迹方程,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 .
. +
+ =1(m>0)的左、右焦点,点P⊆C且
=1(m>0)的左、右焦点,点P⊆C且 •
• =0,|
=0,| |•|
|•| |=4(1)求椭圆C的方程;
|=4(1)求椭圆C的方程; |=
|= |
| |,求动点Q的轨迹方程.
|,求动点Q的轨迹方程.