题目内容
设n为正整数,f(n)=1+
+
+…+
,经计算得f(2)=
,f(4)>2,f(8)>
,f(16)>3,f(32)>
,观察上述结果,对任意正整数n,可推测出一般结论是 .
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
分析:已知的式子可化为f(21)=
,f(22)>
,f(23)>
,f(24)>
,f(25)>
,由此规律可得f(2n)≥
| 1+2 |
| 2 |
| 2+2 |
| 2 |
| 3+2 |
| 2 |
| 4+2 |
| 2 |
| 5+2 |
| 2 |
| n+2 |
| 2 |
解答:解:由题意f(2)=
可化为f(21)=
,
同理f(4)>2可化为f(22)>
,
f(8)>
可化为f(23)>
,
f(16)>3可化为f(24)>
,
f(32)>
可化为f(25)>
,
以此类推,可得f(2n)≥
,
故答案为:f(2n)≥
| 3 |
| 2 |
| 1+2 |
| 2 |
同理f(4)>2可化为f(22)>
| 2+2 |
| 2 |
f(8)>
| 5 |
| 2 |
| 3+2 |
| 2 |
f(16)>3可化为f(24)>
| 4+2 |
| 2 |
f(32)>
| 7 |
| 2 |
| 5+2 |
| 2 |
以此类推,可得f(2n)≥
| n+2 |
| 2 |
故答案为:f(2n)≥
| n+2 |
| 2 |
点评:本题考查归纳推理,把已知的式子变形找规律是解决问题的关键,属基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
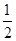 +
+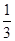 +…+
+…+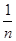 ,计算得f(2)=
,计算得f(2)=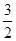 ,f(4)>2,f(8)>
,f(4)>2,f(8)> 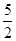 ,f(16)>3,观察上述结果,可推测一般的结论为_________________.
,f(16)>3,观察上述结果,可推测一般的结论为_________________.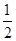 +
+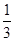 +…+
+…+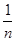 ,计算得f(2)=
,计算得f(2)=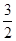 ,f(4)>2,f(8)>
,f(4)>2,f(8)> 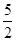 ,f(16)>3,观察上述结果,可推测一般的结论为_________________.
,f(16)>3,观察上述结果,可推测一般的结论为_________________.