题目内容
11.设{an}是公差为d的等差数列,{bn}是公比为q(q≠1)的等比数列.记cn=an+bn.(1)求证:数列{cn+1-cn-d}为等比数列;
(2)已知数列{cn}的前4项分别为4,10,19,34.
①求数列{an}和{bn}的通项公式;
②是否存在元素均为正整数的集合A={n1,n2,…,nk}(k≥4,k∈N*),使得数列${c_{n_1}}$,${c_{n_2}}$,…,${c_{n_k}}$为等差数列?证明你的结论.
分析 (1)依题意,cn+1-cn-d=(an+1+bn+1)-(an+bn)-d=(an+1-an)-d+(bn+1-bn)=bn(q-1)≠0,利用等比数列的定义,即可得出结论;
(2)①由(1)得,等比数列{cn+1-cn-d}的前3项为6-d,9-d,15-d,求出d,q,即可求数列{an}和{bn}的通项公式;
②利用反证法,假设存在满足题意的集合A,不妨设l,m,p,r∈A(l<m<p<r),且cl,cm,cp,cr成等差数列,则2cm=cp+cl,得出cm,cp,cr为数列{cn}的连续三项,从而2cm+1=cm+cm+2,只能q=1,这与q≠1矛盾,即可证明结论.
解答 (1)证明:依题意,cn+1-cn-d=(an+1+bn+1)-(an+bn)-d=(an+1-an)-d+(bn+1-bn)=bn(q-1)≠0,…3分
从而$\frac{{{c_{n+2}}-{c_{n+1}}-d}}{{{c_{n+1}}-{c_n}-d}}=\frac{{{b_{n+1}}(q-1)}}{{{b_n}(q-1)}}=q$,又c2-c1-d=b1(q-1)≠0,
所以{cn+1-cn-d}是首项为b1(q-1),公比为q的等比数列. …5分
(2)解:①由已知条件得,等比数列{cn+1-cn-d}的前3项为6-d,9-d,15-d,
则(9-d)2=(6-d)(15-d),
解得d=3,从而q=2,…7分
且$\left\{\begin{array}{l}{a_1}+{b_1}=4\\{a_1}+3+2{b_1}=10\end{array}\right.$
解得a1=1,b1=3,
所以an=3n-2,${b_n}=3•{2^{n-1}}$. …10分
②假设存在满足题意的集合A,不妨设l,m,p,r∈A(l<m<p<r),且cl,cm,cp,cr成等差数列,
则2cm=cp+cl,
因为cl>0,所以2cm>cp,①
若p>m+1,则p≥m+2,
结合①得,2[(3m-2)+3•2m-1]>(3p-2)+3•2p-1≥3(m+2)-2+3•2m+1,
化简得,${2^m}-m<-\frac{8}{3}<0$,②
因为m≥2,m∈N*,不难知2m-m>0,这与②矛盾,
所以只能p=m+1,
同理,r=p+1,
所以cm,cp,cr为数列{cn}的连续三项,从而2cm+1=cm+cm+2,
即2(am+1+bm+1)=am+bm+am+2+bm+2,
故2bm+1=bm+bm+2,只能q=1,这与q≠1矛盾,
所以假设不成立,从而不存在满足题意的集合A. …16分
点评 本题考查等比数列的判定,考查等差数列、等比数列的通项,考查反证法的运用,考查学生分析解决问题的能力,属于中档题.

| A. | [6,8) | B. | [3,8] | C. | [3,8) | D. | [1,8] |
| 前6小时内的销售量t(单位:件) | 4 | 5 | 6 |
| 频数 | 30 | x | y |
(Ⅱ)若商场每天在购进5件A商品时所获得的平均利润最大,求x的取值范围.
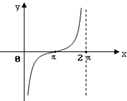
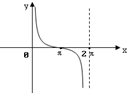
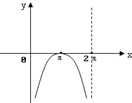
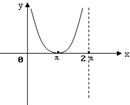
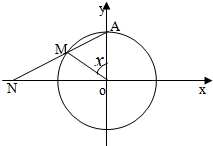 如图,圆x2+y2=1上一定点A(0,1),一动点M从A点开始逆时针绕圆运动一周,并记由射线OA按逆时针方向绕O点旋转到射线OM所形成的∠AOM为x,直线AM与X轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,圆x2+y2=1上一定点A(0,1),一动点M从A点开始逆时针绕圆运动一周,并记由射线OA按逆时针方向绕O点旋转到射线OM所形成的∠AOM为x,直线AM与X轴交于点N(t,0),则函数t=f(x)的图象大致为( )