题目内容
已知命题p:方程a2x2+ax-2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0;
若命题“p或q”是真命题,而命题“p且q”是假命题,且?q是真命题,求a的取值范围.
分析:如果“p或q”为真命题,“p或q”也为真命题,则“p”、“q”中一个为真命题、一个为假命题.然后再分类讨论即可求解.
解答:解:对于命题p:由a2x2+ax-2=0在上有解,
当a=0时,不符合题意;
当a≠0时,方程可化为:(ax+2)(ax-1)=0,
解得:x=-
,或x=
∵x∈[-1,1],
∴-1≤-
≤1或-1≤
≤1,
解得:a≥1或a≤-1
对于命题q:由只有一个实数x满足不等式x2+2ax+2a≤0
得抛物线y=x2+2ax+2a与x轴只有一个交点,
∴△=4a2-8a=0
∴a=0或a=2
又因命题“p或q”是真命题,而命题“p且q”是假命题,且?q是真命题,
则命题p是真命题,命题q是假命题,
所以a的取值范围为(-∞,-1]∪[1,2)∪(2,+∞)
当a=0时,不符合题意;
当a≠0时,方程可化为:(ax+2)(ax-1)=0,
解得:x=-
| 2 |
| a |
| 1 |
| a |
∵x∈[-1,1],
∴-1≤-
| 2 |
| a |
| 1 |
| a |
解得:a≥1或a≤-1
对于命题q:由只有一个实数x满足不等式x2+2ax+2a≤0
得抛物线y=x2+2ax+2a与x轴只有一个交点,
∴△=4a2-8a=0
∴a=0或a=2
又因命题“p或q”是真命题,而命题“p且q”是假命题,且?q是真命题,
则命题p是真命题,命题q是假命题,
所以a的取值范围为(-∞,-1]∪[1,2)∪(2,+∞)
点评:(1)由简单命题和逻辑连接词构成的复合命题的真假可以用真值表来判断,反之根据复合命题的真假也可以判断简单命题的真假.假若p且q真,则p 真,q也真;若p或q真,则p,q至少有一个真;若p且q假,则p,q至少有一个假.(2)可把“p或q”为真命题转化为并集的运算;把“p且q”为真命题转化为交集的运算.

练习册系列答案
相关题目
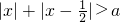 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围. 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围.