题目内容
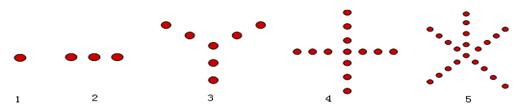
根据图中5个图形及相应点的个数的变化规律,试猜测第8个图中有

57
57
个点.
分析:观察图形点分布的变化规律,发现每一个图形有一个中心点,且从中心点出发的边数在增加,边上的点数也在增加,由此可得结论.
解答:解:观察图形点分布的变化规律,发现第一个图形只有一个中心点;
第二个图形中除中心外还有两边,每边一个点;
第三个图形中除中心点外还有三个边,每边两个点;
依此类推,第n个图形中除中心外有n条边,每边n-1个点,故第n个图形中点的个数为n(n-1)+1=n2-n+1,
当n=8时,n2-n+1=57.
故答案为:57
第二个图形中除中心外还有两边,每边一个点;
第三个图形中除中心点外还有三个边,每边两个点;
依此类推,第n个图形中除中心外有n条边,每边n-1个点,故第n个图形中点的个数为n(n-1)+1=n2-n+1,
当n=8时,n2-n+1=57.
故答案为:57
点评:本题是一道找规律的题目,注意由特殊到一般的分析方法.此题的规律为第n个图中有n2-n+1个点.

练习册系列答案
相关题目
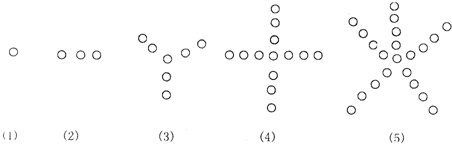
 个图形中的点数
个图形中的点数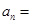 .
.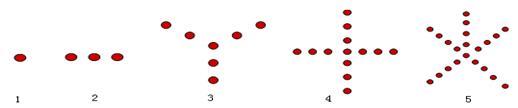
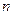 个图形中的点数
个图形中的点数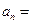 .
.