题目内容
某校高三文科分为五个班.高三数学测试后, 随机地在各班抽取部分学生进行成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了18人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.

(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生,求分数不小于90分的概率.

(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生,求分数不小于90分的概率.
(1)各班被抽取的学生人数分别是18人,19人,20人,21人,22人;
(2)在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率为 .
.
(2)在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率为
 .
.试题分析:(1)先利用频率、样本容量以及总容量之间的关系求出抽取的学生总数,利用各班抽取的人数成等差数列这一条件求出公差,进而确定各班被抽取的人数;(2)在频率分布直方图中找出区间
 所对应的矩形,然后利用频率分布直方图的几何意义计算事件“在抽取的所有学生中,任取一名学生,求分数不小于90分”的概率.
所对应的矩形,然后利用频率分布直方图的几何意义计算事件“在抽取的所有学生中,任取一名学生,求分数不小于90分”的概率.试题解析:(1)由频率分布条形图知,抽取的学生总数为
 人.
人.∵各班被抽取的学生人数成等差数列,设其公差为
 ,
,由
 ="100," 解得
="100," 解得 .
. ∴各班被抽取的学生人数分别是18人,19人,20人,21人,22人.
(2)在抽取的学生中,任取一名学生, 则分数不小于90分的概率为
0.35+0.25+0.1+0.05=0.75.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 (单位:
(单位: )表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.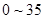





 年
年 月份的
月份的 天中随机抽取
天中随机抽取 天的
天的
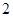 个,设
个,设 为空气质量类别为优或良的天数,求
为空气质量类别为优或良的天数,求


 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的 大小为多少?并说明
大小为多少?并说明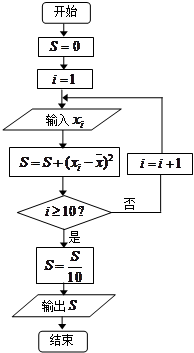


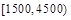 元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图(图左)所示,则该单位职工的月收入的平均数大约是 元.
元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图(图左)所示,则该单位职工的月收入的平均数大约是 元.
 名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩平均分为( )
名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩平均分为( )