题目内容
下列命题中正确的命题是( )A.若
 ,
, ,则
,则 (bn≠0,n∈N*)
(bn≠0,n∈N*)B.若数列{an},{bn}的极限都不存在,则{an+bn}的极限也不存在
C.若数列{an},{an+bn}的极限都存在,则{bn}的极限也存在
D.设Sn=a1+a2+…an,若数列{an}的极限存在,则数列{Sn}的极限也存在
【答案】分析:通过给变量取特殊值、举反例,再利用数列极限的定义和运算,可得选项A、B、D不正确,利用数列极限的运算法则可得C正确.
解答:解:A不正确,当B=0时,则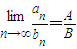 无意义.
无意义.
B不正确,例如当 an =n,bn =-n 时,数列{an},{bn}的极限都不存在,
但{an+bn}是{0},显然极限存在.
C正确,设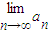 =A,
=A,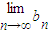 =B,
=B,
则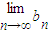 =
=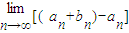 =
= -
-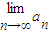 =B-A.
=B-A.
D不正确,当an=2 时,数列{an}的极限存在,但由于Sn=2n,故数列{Sn}的极限不存在.
故选:C.
点评:本题主要考查数列极限的定义和运算,数列极限的运算法则的应用,利用特殊值代入法,排除不符合条件的选项,是一种简单有效的方法.
解答:解:A不正确,当B=0时,则
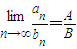 无意义.
无意义.B不正确,例如当 an =n,bn =-n 时,数列{an},{bn}的极限都不存在,
但{an+bn}是{0},显然极限存在.
C正确,设
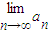 =A,
=A,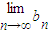 =B,
=B,则
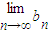 =
=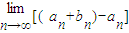 =
= -
-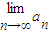 =B-A.
=B-A.D不正确,当an=2 时,数列{an}的极限存在,但由于Sn=2n,故数列{Sn}的极限不存在.
故选:C.
点评:本题主要考查数列极限的定义和运算,数列极限的运算法则的应用,利用特殊值代入法,排除不符合条件的选项,是一种简单有效的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 所成的角相等,那么a∥b
所成的角相等,那么a∥b