题目内容
定义在R上的函数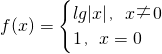
，关于x的方程f（x）=c（c为常数）
恰有三个不同的实数根x1，x2，x3，则x1+x2+x3=________．
0
分析：方程的根，转化为两个函数图象的交点，推出三个根：一个为0，另外两个互为相反数，即可．
解答：关于x的方程f（x）=c（c为常数）恰有三个不同的实数根x1，x2，x3，
令函数y=f（x）和y=c，则两个函数由3个不同交点，又f（x）=lg|x|是偶函数，
在x＞0时是单调增函数，所以c=1，实数根x1，x2，x3，一个为0，另外两个互为相反数，
所以x1+x2+x3=0
故答案为：0
点评：本题考查根的存在性以及根的个数判断，函数的图象等知识，是中档题．
分析：方程的根，转化为两个函数图象的交点，推出三个根：一个为0，另外两个互为相反数，即可．
解答：关于x的方程f（x）=c（c为常数）恰有三个不同的实数根x1，x2，x3，
令函数y=f（x）和y=c，则两个函数由3个不同交点，又f（x）=lg|x|是偶函数，
在x＞0时是单调增函数，所以c=1，实数根x1，x2，x3，一个为0，另外两个互为相反数，
所以x1+x2+x3=0
故答案为：0
点评：本题考查根的存在性以及根的个数判断，函数的图象等知识，是中档题．
练习册系列答案
相关题目
下列四个命题：
是奇函数，则
的图象关于点A（1，0）对称；
则函数
的图象于关直线x=1对称.