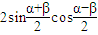题目内容
例3:已知△ABC的三个内角A、B、C成等差数列,a,b,c分别为角A、B、C的对应边,求证1<| a+c |
| b |
| α+β |
| 2 |
| α-β |
| 2 |
| α+β |
| 2 |
| α-β |
| 2 |
分析:先通过A、B、C成等差数列求出B=60°,再通过正弦定理用角表示出
,化简得
=2cos(
),,进而求出A,C的取值范围,求出
的范围.根据余弦函数的单调性得出结果.
| a+c |
| b |
| a+c |
| b |
| A-C |
| 2 |
| A-C |
| 2 |
解答:证明:根据正弦定理a=2rsinA,b=2rsinB,c=2rsinC,
∴
=
=
=
=
∵A、B、C成等差数列
∴A+C=2B
∴A+C+B=3B=180°
∴B=60°
∴
=
=
=2cos(
)
∵A+C+B=180°
∴A=180°-60°-C=120°-C,,C=180°-60°-A=120°-A
∴0<A<120°,0<C<120°
∴-60°<
<60°
∴
<cos(
)≤1
∴1<
=2cos(
)≤2
即1<
≤2
∴
| a+c |
| b |
| sinA+sinC |
| sinC |
2sin(
| ||||
2sin
|
2cos(
| ||||
2sin
|
cos(
| ||
sin
|
∵A、B、C成等差数列
∴A+C=2B
∴A+C+B=3B=180°
∴B=60°
∴
| a+c |
| b |
cos(
| ||
sin
|
cos(
| ||
|
| A-C |
| 2 |
∵A+C+B=180°
∴A=180°-60°-C=120°-C,,C=180°-60°-A=120°-A
∴0<A<120°,0<C<120°
∴-60°<
| A-C |
| 2 |
∴
| 1 |
| 2 |
| A-C |
| 2 |
∴1<
| a+c |
| b |
| A-C |
| 2 |
即1<
| a+c |
| b |
点评:本题主要考查正弦定理的运用.证明本题的关键是通过正弦定理完成边、角问题的转化.

练习册系列答案
相关题目
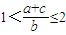 (可能用到的公式:cosα+cosβ=
(可能用到的公式:cosα+cosβ=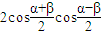 ,sinα+sinβ=
,sinα+sinβ=