题目内容
设函数f(x)=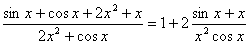
的最大值与最小值分别为M,N,则（ ）A.M-N=4 B.M+N=4 C.M-N=2 D.M+N=2
D
解析:f(x)=,设g(x)=f(x)-1=
,
则g(x)为奇函数，其最大值与最小值分别为g(x0)=M-1,g(-x0)=N-1,
∴g(x0)+g(-x0)=0M+N-2=0,即M+N=2.
练习册系列答案
相关题目
的最大值与最小值分别为M,N,则（ ）题目内容
设函数f(x)=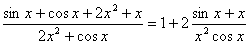的最大值与最小值分别为M,N,则（ ）A.M-N=4 B.M+N=4 C.M-N=2 D.M+N=2
D
解析:f(x)=,设g(x)=f(x)-1=,
则g(x)为奇函数，其最大值与最小值分别为g(x0)=M-1,g(-x0)=N-1,
∴g(x0)+g(-x0)=0M+N-2=0,即M+N=2.
的最大值是________．
的最大值是________．
的最大值，并求出相应的x值．
，则函数f(x)＝
的最小值为
的最大值为M，最小值为m，则M＋m＝________．