题目内容
为进一步推动“学雷锋”活动,弘扬中华民族传统美德,为共建“和谐社会”做出新的贡献.南山中学高三师生响应学校号召,准备在绵阳三诊后集中开展纪念学习雷锋四十七周年的活动.报名参加活动的学生和教师的人数之比为5:1,学校决定按分层抽样的方法从报名的师生中抽取60人组队进行活动.已知教师甲被抽到的概率为 ,则报名的学生人数是
,则报名的学生人数是
- A.100
- B.500
- C.10
- D.50
B
分析:令学生有5x人,则老师有x人,根据抽取的老师数为 60×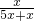 =10人,求出老师的总人数,从而求得报名的学生人数.
=10人,求出老师的总人数,从而求得报名的学生人数.
解答:令学生有5x人,则老师有x人,于是得到老师要抽取 60×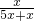 =10人,所以老师共有100人,故学生有500人,
=10人,所以老师共有100人,故学生有500人,
故选B.
点评:本题主要考查分层抽样的定义和方法,按每层个体数所占的比例抽取样本数,注意抽样过程中每个个体被抽到的可能性相同,属于基础题.
分析:令学生有5x人,则老师有x人,根据抽取的老师数为 60×
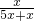 =10人,求出老师的总人数,从而求得报名的学生人数.
=10人,求出老师的总人数,从而求得报名的学生人数.解答:令学生有5x人,则老师有x人,于是得到老师要抽取 60×
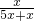 =10人,所以老师共有100人,故学生有500人,
=10人,所以老师共有100人,故学生有500人,故选B.
点评:本题主要考查分层抽样的定义和方法,按每层个体数所占的比例抽取样本数,注意抽样过程中每个个体被抽到的可能性相同,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 ,则报名的学生人数是( )
,则报名的学生人数是( )