题目内容
如图所示,矩形ABCD的边AB=a,BC=2,PA⊥平面ABCD,PA=2,现有数据:①
 ;②a=1;③
;②a=1;③ ;建立适当的空间直角坐标系,
;建立适当的空间直角坐标系,( I)当BC边上存在点Q,使PQ⊥QD时,a可能取所给数据中的哪些值?请说明理由;
( II)在满足( I)的条件下,若a取所给数据的最小值时,这样的点Q有几个?若沿BC方向依次记为Q1,Q2,…,试求二面角Q1-PA-Q2的大小.

【答案】分析:( I)建立空间直角坐标系,求出各点的坐标,设出点Q的坐标,进而得到向量PQ,QD的坐标,再结合PQ⊥QD即可求出结论;
( II) 由(Ⅰ)知 ,此时
,此时 或
或 ,即满足条件的点Q有两个;再结合PA⊥平面ABCD即可得到∠Q1AQ2就是二面角Q1-PA-Q2的平面角,再代入向量的夹角计算公式即可.
,即满足条件的点Q有两个;再结合PA⊥平面ABCD即可得到∠Q1AQ2就是二面角Q1-PA-Q2的平面角,再代入向量的夹角计算公式即可.
解答: 解:( I)建立如图所示的空间直角坐标系,则各点坐标分别为:
解:( I)建立如图所示的空间直角坐标系,则各点坐标分别为:
A(0,0,0),B(a,0,0),C(a,2,0),D(0,2,0),P(0,0,2)
设Q(a,x,0)(0≤x≤2),…(2分)
∵ ,
,
∴由PQ⊥QD得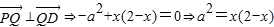 .
.
∵x∈[0,2],a2=x(2-x)∈(0,1]…(4分)
∴在所给数据中,a可取 和a=1两个值.…(6分)
和a=1两个值.…(6分)
( II) 由(Ⅰ)知 ,此时
,此时 或
或 ,即满足条件的点Q有两个,…(8分)
,即满足条件的点Q有两个,…(8分)
 根据题意,其坐标为
根据题意,其坐标为 和
和 ,…(9分)
,…(9分)
∵PA⊥平面ABCD,
∴PA⊥AQ1,PA⊥AQ2,
∴∠Q1AQ2就是二面角Q1-PA-Q2的平面角.…(10分)
由 =
=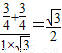 ,
,
得∠Q1AQ2=30°,
∴二面角Q1-PA-Q2的大小为30°.…(12分)
点评:本题主要考察直线与平面所成的角.解决本题第一问的关键在于结合二次函数的性质得到a可取 和a=1两个值.
和a=1两个值.
( II) 由(Ⅰ)知
 ,此时
,此时 或
或 ,即满足条件的点Q有两个;再结合PA⊥平面ABCD即可得到∠Q1AQ2就是二面角Q1-PA-Q2的平面角,再代入向量的夹角计算公式即可.
,即满足条件的点Q有两个;再结合PA⊥平面ABCD即可得到∠Q1AQ2就是二面角Q1-PA-Q2的平面角,再代入向量的夹角计算公式即可.解答:
 解:( I)建立如图所示的空间直角坐标系,则各点坐标分别为:
解:( I)建立如图所示的空间直角坐标系,则各点坐标分别为:A(0,0,0),B(a,0,0),C(a,2,0),D(0,2,0),P(0,0,2)
设Q(a,x,0)(0≤x≤2),…(2分)
∵
 ,
,∴由PQ⊥QD得
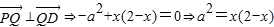 .
.∵x∈[0,2],a2=x(2-x)∈(0,1]…(4分)
∴在所给数据中,a可取
 和a=1两个值.…(6分)
和a=1两个值.…(6分)( II) 由(Ⅰ)知
 ,此时
,此时 或
或 ,即满足条件的点Q有两个,…(8分)
,即满足条件的点Q有两个,…(8分) 根据题意,其坐标为
根据题意,其坐标为 和
和 ,…(9分)
,…(9分)∵PA⊥平面ABCD,
∴PA⊥AQ1,PA⊥AQ2,
∴∠Q1AQ2就是二面角Q1-PA-Q2的平面角.…(10分)
由
 =
=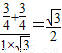 ,
,得∠Q1AQ2=30°,
∴二面角Q1-PA-Q2的大小为30°.…(12分)
点评:本题主要考察直线与平面所成的角.解决本题第一问的关键在于结合二次函数的性质得到a可取
 和a=1两个值.
和a=1两个值. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
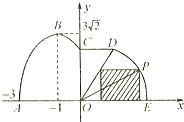 如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB= 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB= <φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3
<φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3 );赛道的中间部分为
);赛道的中间部分为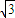 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.
 (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.
 ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时