题目内容
若等差数列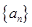 的前15项的和为定值,则下列几项中为定值的是________.
的前15项的和为定值,则下列几项中为定值的是________.
①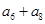 ;②
;②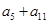 ;③
;③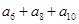 ;④
;④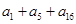 ;⑤
;⑤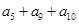 .
.
②③⑤
解析试题分析:根据等差数列{an}的前15项的和为定值得到a1+a15是定值,或a8是定值,把下面的五个式子根据等差数列的性质变化,变化为与前面得到的两个定值能比较的形式,选出可以是定值的式子.解:∵等差数列{an}的前15项的和为定值,∴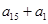 是定值, a8是定值,,①
是定值, a8是定值,,①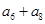 ≠
≠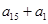 ,故①不是定值,②
,故①不是定值,②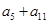 =
=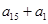 ,故②是定值,③
,故②是定值,③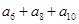 =a
=a ,故③是定值,④
,故③是定值,④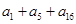 =3a1+19d≠3a8,故④不是定值,⑤
=3a1+19d≠3a8,故④不是定值,⑤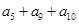 =3a1+21d=3a8,故⑤是定值,综上可知②③⑤是定值,故答案为:②③⑤
=3a1+21d=3a8,故⑤是定值,综上可知②③⑤是定值,故答案为:②③⑤
考点:等差数列的性质
点评:本题没有具体的数字运算,它考查的是等差数列的性质,有数列的等差中项,等差数列的前n项和,实际上这类问题比具体的数字运算要困难,对同学们来说有些抽象

练习册系列答案
相关题目
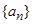 中,若
中,若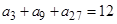 ,则
,则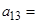 .
.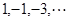 的第 项.
的第 项.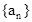 中,已知前15项的和
中,已知前15项的和 ,则
,则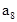 等于_____________
等于_____________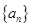 的前
的前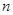 项和为
项和为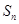 ,
,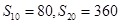 ,则
,则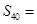 ;
; 的前n项和为
的前n项和为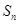 ,且
,且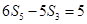 ,则
,则 =________.
=________.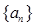 为等差数列,若
为等差数列,若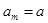 ,
,
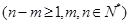 ,则
,则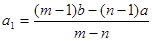 .类比上述结论,对于等比数列
.类比上述结论,对于等比数列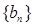
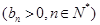 ,若
,若
 ,则可以得到
,则可以得到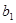 =____________.
=____________.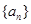 中,有
中,有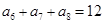 ,则此数列的前13项之和为 .
,则此数列的前13项之和为 .  中,
中,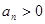 ,且
,且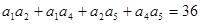 ,则
,则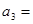 .
.