题目内容
已知椭圆C焦点在x轴上,其长轴长为4,离心率为 ,
,(1)设过定点M(0,2)的直线l与椭圆C交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围;
(2)如图,过原点O任意作两条互相垂直的直线与椭圆
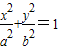 (a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR一边的距离为d,试求d=1时a,b满足的条件.
【答案】分析:(1)由题设知 .由此得
.由此得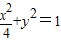 .设直线l:y=kx+2,A(x1,y1),B(x2,y2).由
.设直线l:y=kx+2,A(x1,y1),B(x2,y2).由 得(1+4k2)x2+16kx+12=0.由△=(16k)2-4×12(1+4k2)>0,知
得(1+4k2)x2+16kx+12=0.由△=(16k)2-4×12(1+4k2)>0,知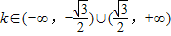 .又
.又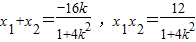 ,由
,由 .得-2<k<2.由此得:
.得-2<k<2.由此得: .
.
(2)由椭圆的对称性可知PQSR是菱形,原点O到各边的距离相等.当P在y轴上,Q在x轴上时,直线PQ的方程为 ,由d=1得
,由d=1得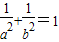 ,当P不在y轴上时,设直线PS的斜率为k,P(x1,kx1),则直线RQ的斜率为
,当P不在y轴上时,设直线PS的斜率为k,P(x1,kx1),则直线RQ的斜率为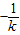 ,
,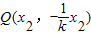 由
由 ,得
,得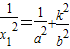 (1),同理
(1),同理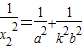 .由此知a,b满足条件
.由此知a,b满足条件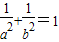 .
.
解答:解:(1)∵椭圆C焦点在x轴上,其长轴长为4,离心率为 ,
,
∴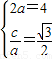 .解得a=2,b=1,∴
.解得a=2,b=1,∴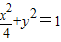
显然直线x=0不满足题设条件,可设直线l:y=kx+2,A(x1,y1),B(x2,y2).(5分)
由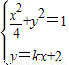 得(1+4k2)x2+16kx+12=0.∵△=(16k)2-4×12(1+4k2)>0,
得(1+4k2)x2+16kx+12=0.∵△=(16k)2-4×12(1+4k2)>0,
∴
又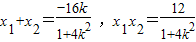
由 .∴
.∴ .
.
所以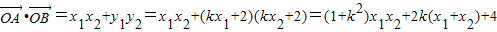 =
=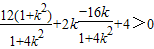 ∴-2<k<2.
∴-2<k<2.
由此得: .
.
(2)由椭圆的对称性可知PQSR是菱形,原点O到各边的距离相等.
当P在y轴上,Q在x轴上时,直线PQ的方程为 ,由d=1得
,由d=1得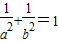 ,
,
当P不在y轴上时,设直线PS的斜率为k,P(x1,kx1),则直线RQ的斜率为 ,
,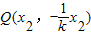
由 ,得
,得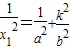 (1),同理
(1),同理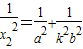
在Rt△OPQ中,由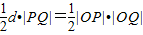 ,即|PQ|2=|OP|2•|OQ|2
,即|PQ|2=|OP|2•|OQ|2
所以 ,化简得
,化简得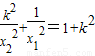 ,
,
分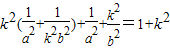 ,
,
即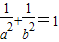 .
.
综上,d=1时a,b满足条件
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
 .由此得
.由此得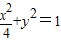 .设直线l:y=kx+2,A(x1,y1),B(x2,y2).由
.设直线l:y=kx+2,A(x1,y1),B(x2,y2).由 得(1+4k2)x2+16kx+12=0.由△=(16k)2-4×12(1+4k2)>0,知
得(1+4k2)x2+16kx+12=0.由△=(16k)2-4×12(1+4k2)>0,知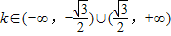 .又
.又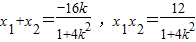 ,由
,由 .得-2<k<2.由此得:
.得-2<k<2.由此得: .
.(2)由椭圆的对称性可知PQSR是菱形,原点O到各边的距离相等.当P在y轴上,Q在x轴上时,直线PQ的方程为
 ,由d=1得
,由d=1得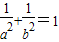 ,当P不在y轴上时,设直线PS的斜率为k,P(x1,kx1),则直线RQ的斜率为
,当P不在y轴上时,设直线PS的斜率为k,P(x1,kx1),则直线RQ的斜率为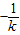 ,
,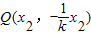 由
由 ,得
,得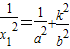 (1),同理
(1),同理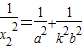 .由此知a,b满足条件
.由此知a,b满足条件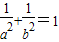 .
.解答:解:(1)∵椭圆C焦点在x轴上,其长轴长为4,离心率为
 ,
,∴
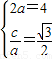 .解得a=2,b=1,∴
.解得a=2,b=1,∴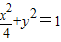
显然直线x=0不满足题设条件,可设直线l:y=kx+2,A(x1,y1),B(x2,y2).(5分)
由
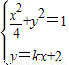 得(1+4k2)x2+16kx+12=0.∵△=(16k)2-4×12(1+4k2)>0,
得(1+4k2)x2+16kx+12=0.∵△=(16k)2-4×12(1+4k2)>0,∴

又
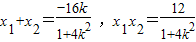
由
 .∴
.∴ .
.所以
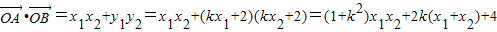 =
=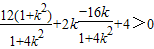 ∴-2<k<2.
∴-2<k<2.由此得:
 .
.(2)由椭圆的对称性可知PQSR是菱形,原点O到各边的距离相等.
当P在y轴上,Q在x轴上时,直线PQ的方程为
 ,由d=1得
,由d=1得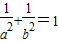 ,
,当P不在y轴上时,设直线PS的斜率为k,P(x1,kx1),则直线RQ的斜率为
 ,
,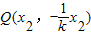
由
 ,得
,得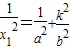 (1),同理
(1),同理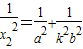
在Rt△OPQ中,由
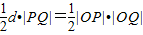 ,即|PQ|2=|OP|2•|OQ|2
,即|PQ|2=|OP|2•|OQ|2所以
 ,化简得
,化简得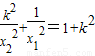 ,
,分
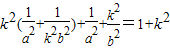 ,
,即
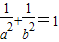 .
.综上,d=1时a,b满足条件

点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目