题目内容
（2008•广东）在平行四边形ABCD中，AC与DB交于点O，E是线段OD的中点，AE延长线与CD交于F．若
=
，
=
，则
=（ ）
| AC |
| a |
| BD |
| b |
| AF |
分析：根据两个三角形相似对应边成比例，得到DF与FC之比，做FG平行BD交AC于点G，使用已知向量表示出要求的向量，
得到结果．
得到结果．
解答：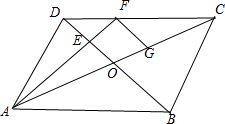
解：∵由题意可得△DEF∽△BEA，
∴
=
=
，再由AB=CD可得
=
，
∴
=
．
作FG平行BD交AC于点G，
∴
=
=
，
∴
=
=
=
．
∵
=
+
=
+
=
+
=
=
，
∴
=
+
=
+
，
故选B．
解：∵由题意可得△DEF∽△BEA，∴
| DE |
| EB |
| DF |
| AB |
| 1 |
| 3 |
| DF |
| DC |
| 1 |
| 3 |
∴
| DF |
| FC |
| 1 |
| 2 |
作FG平行BD交AC于点G，
∴
| FG |
| DO |
| CG |
| CO |
| 2 |
| 3 |
∴
| GF |
| 2 |
| 3 |
| OD |
| 1 |
| 3 |
| BD |
| 1 |
| 3 |
| b |
∵
| AG |
| AO |
| OG |
| AO |
| 1 |
| 3 |
| OC |
| 1 |
| 2 |
| AC |
| 1 |
| 6 |
| AC |
| 2 |
| 3 |
| AC |
| 2 |
| 3 |
| a |
∴
| AF |
| AG |
| GF |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
故选B．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，向量是数形结合的典型例子，向量的加减运算是用向量解决问题的基础，要学好运算，才能用向量解决立体几何问题，三角函数问题，好多问题都是以向量为载体的，本题属于中档题．
练习册系列答案
相关题目
B B.B
的坐标分别是
，
，直线
相交于点M，且它们的斜率之积为
．
的方程；
的直线
与（1）中的轨迹
、
（
、
与
面积之比的取值范围（
为坐标原点）．
B B.B
B B.B