题目内容
已知定义域为（O，+∞）的单调函数f（x），若对任意x∈（0，+∞），都有f[f（x）+
]=3”，则方程f（x）=2+
的解的个数是（ ）A．3
B．2
C．1
D．O
【答案】分析：由题设知必存在唯一的正实数a，满足
，f（a）=3，
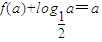，故3+
，
，
，左增，右减，有唯一解a=2，故
，由此能够导出方程f（x）=2+
的解的个数是2．
解答：解：∵定义域为（O，+∞）的单调函数f（x），
满足f[f（x）+
]=3，f（x）=2+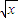
，
∴必存在唯一的正实数a，
满足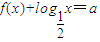
，f（a）=3，①
∴
，②
由①②得：3+
，
，
，左增，右减，有唯一解a=2，
故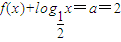
，
f（x）=2-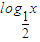
，
由2-
=2+
，得
，
∴
，
令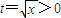
，则t2=2t，
此方程只有两个正根t=2，或t=4，
∴x=4，或x=16．
故方程f（x）=2+
的解的个数是2．
故选B．
点评：本题考查对数的运算性质的综合运用，综合性强，难度大．解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化．
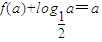，f（a）=3，，故3+，，，左增，右减，有唯一解a=2，故，由此能够导出方程f（x）=2+的解的个数是2．解答：解：∵定义域为（O，+∞）的单调函数f（x），
满足f[f（x）+
]=3，f（x）=2+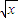，∴必存在唯一的正实数a，
满足
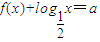，f（a）=3，①∴
，②由①②得：3+
，，，左增，右减，有唯一解a=2，故
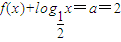，f（x）=2-
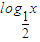，由2-
=2+，得，∴
，令
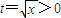，则t2=2t，此方程只有两个正根t=2，或t=4，
∴x=4，或x=16．
故方程f（x）=2+
的解的个数是2．故选B．
点评：本题考查对数的运算性质的综合运用，综合性强，难度大．解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化．
练习册系列答案
阅读快车系列答案
相关题目