题目内容
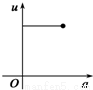
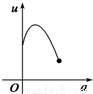
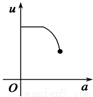
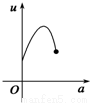
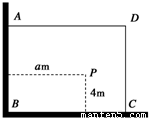
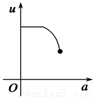
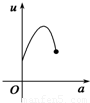
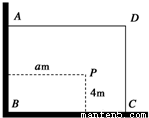
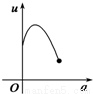
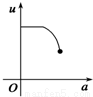
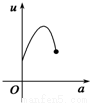
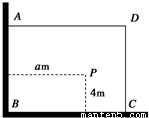
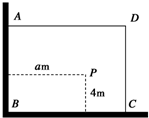 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )A、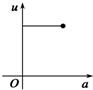 | B、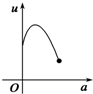 | C、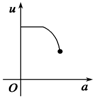 | D、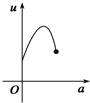 |
分析:为求矩形ABCD面积的最大值S,可先将其面积表达出来,又要注意P点在长方形ABCD内,所以要注意分析自变量的取值范围,并以自变量的限制条件为分类标准进行分类讨论.
解答:解:设AD长为x,则CD长为16-x
又因为要将P点围在矩形ABCD内,
∴a≤x≤12
则矩形ABCD的面积为x(16-x),
当0<a≤8时,当且仅当x=8时,S=64
当8<a<12时,S=a(16-a)
S=
分段画出函数图形可得其形状与C接近
故选C.
又因为要将P点围在矩形ABCD内,
∴a≤x≤12
则矩形ABCD的面积为x(16-x),
当0<a≤8时,当且仅当x=8时,S=64
当8<a<12时,S=a(16-a)
S=
|
分段画出函数图形可得其形状与C接近
故选C.
点评:解决本题的关键是将S的表达式求出来,结合自变量的取值范围,分类讨论后求出S的解析式.

练习册系列答案
相关题目
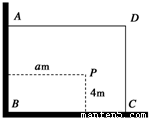 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )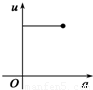
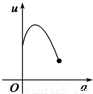

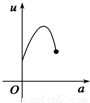
 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )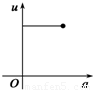
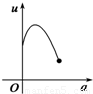
 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )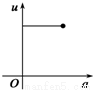
 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )