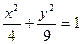题目内容
设集合A={1,2,3,4},m,n∈A,则方程 表示焦点在x轴上的椭圆有
表示焦点在x轴上的椭圆有
| A.6个 | B.8个 | C.12个 | D.16个 |
A
解析

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
若椭圆的对称轴为坐标轴,长轴长为10,焦距为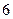 ,则椭圆的方程为
,则椭圆的方程为
A.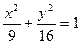 | B.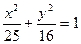 | C.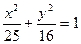 或 或 | D.以上都不对 |
椭圆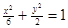 和双曲线
和双曲线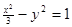 的公共点为
的公共点为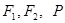 是两曲线的一个交点, 那么
是两曲线的一个交点, 那么 的值是
的值是
A.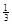 | B.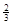 | C.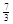 | D.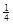 |
(文科)双曲线 的离心率是2,则k的值是( )
的离心率是2,则k的值是( )
| A.12 | B.4 | C.—12 | D.—4 |
若抛物线 上一点
上一点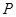 到其焦点的距离为
到其焦点的距离为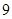 ,则点
,则点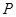 的坐标为( )
的坐标为( )
A.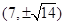 | B.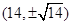 | C.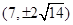 | D.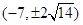 |
对抛物线 ,下列描述正确的是( )
,下列描述正确的是( )
A.开口向上,焦点为 | B.开口向上,焦点为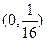 |
C.开口向右,焦点为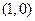 | D.开口向右,焦点为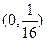 |
若椭圆 和双曲线
和双曲线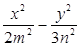 =1有公共的焦点,则双曲线的渐近线方程是
=1有公共的焦点,则双曲线的渐近线方程是
A.x=±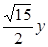 | B.y=±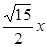 | C.x=± 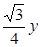 | D.y=± |
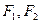 分别为双曲线
分别为双曲线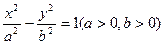 的左、右焦点,若在双曲线右支上存在点
的左、右焦点,若在双曲线右支上存在点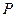 ,满足
,满足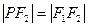 ,且
,且 到直线
到直线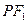 的距离等于双曲线的实轴长,则该双曲线的渐进线方程为 ( )
的距离等于双曲线的实轴长,则该双曲线的渐进线方程为 ( )
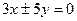
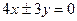
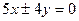
 上的动点, 作PD⊥y轴, D为垂足, 则PD中点的轨迹方程为 ( )
上的动点, 作PD⊥y轴, D为垂足, 则PD中点的轨迹方程为 ( )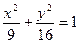 B
B  C
C 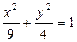 D
D