题目内容
已知A={x|2a≤x≤a2+1},B={x|x2-3(a+1)x+2(3a+1)≤0},若A?B,求实数a的范围.
解：设f(x)=x2-3(a+1)x+2(3a+1)，
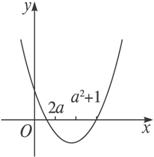
∵A
B,∴f(x)在［2a,a2+1］上的图象全部落在x轴下方，如图所示，
则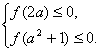
即
∴
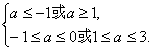
∴a的取值范围是{a|a=-1或1≤a≤3}.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
口算题卡北京妇女儿童出版社系列答案题目内容
已知A={x|2a≤x≤a2+1},B={x|x2-3(a+1)x+2(3a+1)≤0},若A?B,求实数a的范围.
解：设f(x)=x2-3(a+1)x+2(3a+1)，
∵AB,∴f(x)在［2a,a2+1］上的图象全部落在x轴下方，如图所示，
则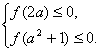
即
∴
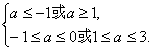
∴a的取值范围是{a|a=-1或1≤a≤3}.
口算题卡北京妇女儿童出版社系列答案