题目内容
8.已知函数f(x)=x2+2x+a,g(x)=$\frac{f(x)}{x}$,(1)若不等式f(x)<0的解集是{x|a<x<1},求a的值;
(2)若x<0,a=4,求函数g(x)的最大值;
(3)若对任意x∈[1,+∞),不等式g(x)>0恒成立,求实数a的取值范围.
分析 (1)由不等式f(x)<0的解集是{x|a<x<1}知,a和1是方程x2+2x+a=0的根,代人求a
(2)利用a+b≥2$\sqrt{ab}$(a,b为正数)定理,对式子变形求解
(3)等价转换,把恒成立问题转换成最值问题解决
解答 解:由题知f(1)=0,
∴1+2+a=0
∴a=-3
(2)g(x)=$\frac{{x}^{2}+2x+4}{x}$=x+$\frac{4}{x}$+2
当x<0时,-x>0
∴-x+$\frac{4}{-x}$≥4
∴x+$\frac{4}{x}$+2≤-2
故g(x)的最大值为-2
(3)g(x)>0恒成立 x∈[1,+∞)
∴f(x)=x2+2x+a>0恒成立 x∈[1,+∞)
∴a>-(x2+2x)恒成立
令h(x)=-(x2+2x)
∴h(x)≤h(1)=-3
∴a>-3
点评 考察了不等式与方程的关系,两个正数的算术平均数不小于几何平均数定理和恒成立问题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
12.函数f(x)=$\frac{2x+1}{x-1}$的单调递减区间是( )
| A. | (-∞,1)∪(1,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,0),(0,+∞) | D. | (-∞,1),(1,+∞) |
 ,集合
,集合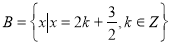
 B.
B.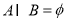 C.
C.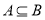 D.
D.
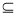 B,则实数a的取值范围是
B,则实数a的取值范围是 表示成列举法,正确的是
表示成列举法,正确的是