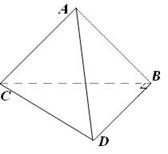
题目内容
如图,平面ACB⊥平面BCD,∠CAB=∠CBD=900, ∠BDC=600,BC=6,AB=AC.
(Ⅰ)求证:平面ABD⊥平面ACD;(Ⅱ)求二面角A—CD—B的平面角的正切值;
(Ⅲ)设过直线AD且与BC平行的平面为![]() ,求点B到平面
,求点B到平面![]() 的距离。
的距离。
(1)证明见解析(2) 2(3)![]()
解析:
(Ⅰ)证明 ∵平面ACB⊥平面BCD,∠CBD=900,
∴DB⊥平面ACB, ∴DB⊥CA.又∠CAB=900,∴CA⊥平面ADB
∴平面ACB⊥平面BCD. ——————————4分
(Ⅱ)解 设BC的中点为E,作EF⊥CD,垂足为F,连结AF。
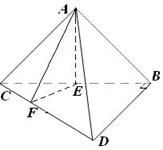
∵AC=AB,∴AE⊥BC,∵平面ACB⊥平面BCD, ∴AE⊥平面BCD,
∴FE是AF在平面BCD内的射影,
∴AF⊥CD,
即∠AFE就是二面角A—CD—B的平面角。 ———————6分
在等腰直角△ABC中,斜边BC=6, ∴AE=3,且CE=3,
在Rt△CEF中,∠ECF=300, ∴EF=![]() ,
,
∴tan∠AFE=![]() ,即二面角A—CD—B的平面角的正切值是2. ———————8分
,即二面角A—CD—B的平面角的正切值是2. ———————8分
(Ⅲ)解 如图,设DC的中点为G,分别以直线EG.EB.EA为x.y.z轴,建立空间直角坐标系E—xyz.
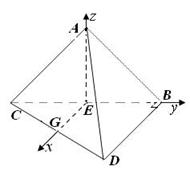
∴A(0,0,3),B(0,3,0),D(![]() ,3,0)
,3,0)
![]() ,
,![]() ,
,![]()
设过AD和BC平行的平面![]() 的一个法向量是n=(a,b,c),则有
的一个法向量是n=(a,b,c),则有
![]() 且
且![]() ,即
,即
![]() 且3b=0,取
且3b=0,取![]() 得n=
得n=![]() ,
,
∴点B到![]() 的距离d=
的距离d=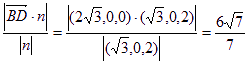 。 ———————12分
。 ———————12分

练习册系列答案
相关题目
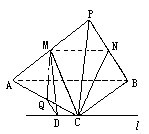
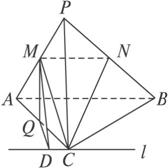
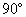 ,∠B=
,∠B=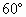 ,PC⊥平面ABC,AB=8,PC=6,M,N分别是PA,PB的中点,设△MNC所在平面与△ABC所在平面交于直线l.(1)判断l与MN的位置关系;(2)求点M到l的距离.
,PC⊥平面ABC,AB=8,PC=6,M,N分别是PA,PB的中点,设△MNC所在平面与△ABC所在平面交于直线l.(1)判断l与MN的位置关系;(2)求点M到l的距离.