题目内容
已知数列{an}的前n项和为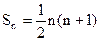
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若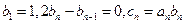 ,数列{Cn}的前项和为Tn,求证:Tn<4.
,数列{Cn}的前项和为Tn,求证:Tn<4.
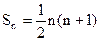
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若
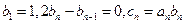 ,数列{Cn}的前项和为Tn,求证:Tn<4.
,数列{Cn}的前项和为Tn,求证:Tn<4.解:(Ⅰ)∵数列{an}的前n项和为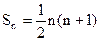
∴当n=1时,a1= S1=1
当n≥2时,an=" Sn-" Sn-1=n
∴an=n
(Ⅱ)由若b1=1,2bn-bn-1=0得
∴{bn}是以b1=1为首项,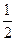 为公比的等比数列.
为公比的等比数列.
∴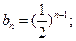
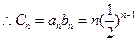
∴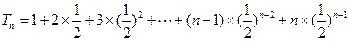
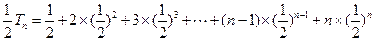
两式相减得: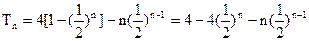
∴ Tn<4
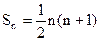
∴当n=1时,a1= S1=1
当n≥2时,an=" Sn-" Sn-1=n
∴an=n
(Ⅱ)由若b1=1,2bn-bn-1=0得

∴{bn}是以b1=1为首项,
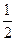 为公比的等比数列.
为公比的等比数列. ∴
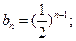
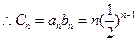
∴
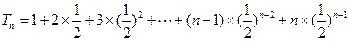
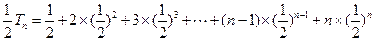
两式相减得:
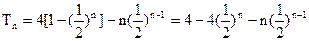
∴ Tn<4

略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
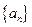 满足:
满足: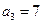 ,
,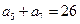 .
.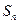
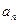 及
及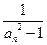 (n
(n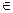 N*),求数列
N*),求数列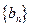 的前n项和
的前n项和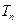 .
.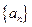 的首项为
的首项为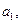 公差为
公差为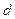 ,前
,前 项的和为
项的和为 ,则数列
,则数列 为等差数列,且通项为
为等差数列,且通项为 .类似地,请完成下列命题:若各项均为正数的等比数列
.类似地,请完成下列命题:若各项均为正数的等比数列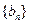 的首项为
的首项为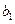 ,公比为
,公比为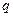 ,前
,前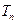 ,则 .
,则 .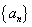 满足
满足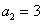 ,
,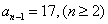 ,
, ,则
,则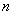 的值为( )
的值为( ) 
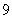
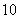

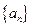 中
中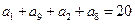 ,则
,则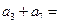 _________.
_________. 等差数列{
等差数列{ 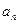 }的前n项和为
}的前n项和为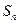 ,且
,且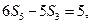
 则
则 =
= 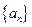 中,已知
中,已知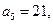 则
则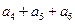 等于( )
等于( ) (n∈N*);则数列{bn}的前50项和为
(n∈N*);则数列{bn}的前50项和为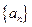 的通项公式为
的通项公式为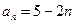 , 则它的公差是
, 则它的公差是