题目内容
已知双曲线W: +
+ =1(a>0,b>0)的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且
=1(a>0,b>0)的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且 •
•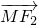 =-1,∠NMF2=120°.
=-1,∠NMF2=120°.
(Ⅰ)求双曲线的方程;
(Ⅱ)过点Q(0,-2)的直线l交双曲线W的右支于A、B两个不同的点,若点H(7,0)在以线段AB为直径的圆的外部,求实数k的取值范围.
解:(Ⅰ)由已知M(a,0),N(0,b),F2(c,0),
∴ •
•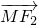 =(-a,b)•(c-a,0)=a2-ac=-1,
=(-a,b)•(c-a,0)=a2-ac=-1,
∵∠NMF2=120°,∴∠NMF1=60°,∴b= a,∴c2-a2=3a2,∴c=2a
a,∴c2-a2=3a2,∴c=2a
∴a=1,b= ,
,
∴双曲线的方程为 .(4分)
.(4分)
(Ⅱ)由题知,直线l的斜率存在且不为0,设为k(k≠0),直线l:y=kx-2,代入双曲线方程,消去y可得
(3-k2)x2+4kx-7=0,(6分)
设A(x1,y1)、B(x2,y2),则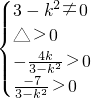 ,解得
,解得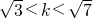 .①(8分)
.①(8分)
∵点H(7,0)在以线段AB为直径的圆的外部,则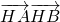 >0,(9分)
>0,(9分)
∴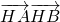 =(x1-7,y1)•(x2-7,y2)=(1+k2)x1x2-(7+2k)(x1+x2)+53
=(x1-7,y1)•(x2-7,y2)=(1+k2)x1x2-(7+2k)(x1+x2)+53
=(1+k2)×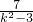 -(7+2k)×
-(7+2k)×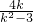 +53=
+53=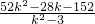 >0
>0
∴k>2 ②(11分)
由①、②得实数k的范围是(2, ).(12分)
).(12分)
分析:(Ⅰ)利用 •
•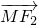 =-1,可得
=-1,可得 •
•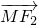 =a2-ac=-1,根据∠NMF2=120°,可得c=2a,由此可求双曲线的方程;
=a2-ac=-1,根据∠NMF2=120°,可得c=2a,由此可求双曲线的方程;
(Ⅱ)设直线l的方程代入双曲线方程,消去y,利用直线l交双曲线W的右支于A、B两个不同的点,确定k的范围,根据点H(7,0)在以线段AB为直径的圆的外部,可得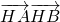 >0,由此可得得实数k的范围.
>0,由此可得得实数k的范围.
点评:本题考查双曲线的标准方程,考查直线与双曲线的位置关系,考查韦达定理的运用,考查向量知识的运用,属于中档题.
∴
 •
•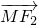 =(-a,b)•(c-a,0)=a2-ac=-1,
=(-a,b)•(c-a,0)=a2-ac=-1,∵∠NMF2=120°,∴∠NMF1=60°,∴b=
 a,∴c2-a2=3a2,∴c=2a
a,∴c2-a2=3a2,∴c=2a∴a=1,b=
 ,
,∴双曲线的方程为
 .(4分)
.(4分)(Ⅱ)由题知,直线l的斜率存在且不为0,设为k(k≠0),直线l:y=kx-2,代入双曲线方程,消去y可得
(3-k2)x2+4kx-7=0,(6分)
设A(x1,y1)、B(x2,y2),则
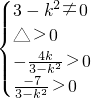 ,解得
,解得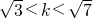 .①(8分)
.①(8分)∵点H(7,0)在以线段AB为直径的圆的外部,则
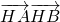 >0,(9分)
>0,(9分)∴
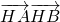 =(x1-7,y1)•(x2-7,y2)=(1+k2)x1x2-(7+2k)(x1+x2)+53
=(x1-7,y1)•(x2-7,y2)=(1+k2)x1x2-(7+2k)(x1+x2)+53=(1+k2)×
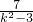 -(7+2k)×
-(7+2k)×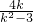 +53=
+53=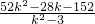 >0
>0∴k>2 ②(11分)
由①、②得实数k的范围是(2,
 ).(12分)
).(12分)分析:(Ⅰ)利用
 •
•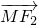 =-1,可得
=-1,可得 •
•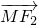 =a2-ac=-1,根据∠NMF2=120°,可得c=2a,由此可求双曲线的方程;
=a2-ac=-1,根据∠NMF2=120°,可得c=2a,由此可求双曲线的方程;(Ⅱ)设直线l的方程代入双曲线方程,消去y,利用直线l交双曲线W的右支于A、B两个不同的点,确定k的范围,根据点H(7,0)在以线段AB为直径的圆的外部,可得
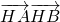 >0,由此可得得实数k的范围.
>0,由此可得得实数k的范围.点评:本题考查双曲线的标准方程,考查直线与双曲线的位置关系,考查韦达定理的运用,考查向量知识的运用,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 +
+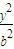 =1(a>0,b>0)的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且
=1(a>0,b>0)的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且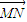 •
•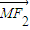 =-1,∠NMF2=120°.
=-1,∠NMF2=120°.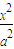 +
+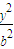 =1(a>0,b>0)的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且
=1(a>0,b>0)的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且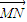 •
• =-1,∠NMF2=120°.
=-1,∠NMF2=120°.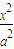 +
+ =1(a>0,b>0)的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且
=1(a>0,b>0)的左、右焦点分别为F1、F2,点N(0,b),右顶点是M,且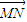 •
• =-1,∠NMF2=120°.
=-1,∠NMF2=120°.