题目内容
例2．已知A={x|x2-3x+2≤0}，B={x|x2-（a+1）x+a≤0}，（1）若A不属于B，求a的取值范围．（2）若B⊆A，求a的取值范围．
解：A={x|1≤x≤2}，
当a＞1时，B={x|1≤x≤a}；当a=1时，B={1}；当a＜1时，B={x|a≤x≤1}．
（1）若A?B，则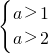
所以a＞2；
（2）若B⊆A，
当a=1时，满足题意；当a＞1时，a≤2，此时1＜a≤2；当a＜1时，不合题意．
所以，a的取值范围为[1，2）．
分析：先化简集合A，在根据条件（1）若A不属于B则，（2）若B⊆A，讨论a的取值范围．
点评：本题主要考查集合间的包含关系，较为简单，只需化简集合A，B计算可，注意分情况讨论．
当a＞1时，B={x|1≤x≤a}；当a=1时，B={1}；当a＜1时，B={x|a≤x≤1}．
（1）若A?B，则
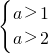所以a＞2；（2）若B⊆A，
当a=1时，满足题意；当a＞1时，a≤2，此时1＜a≤2；当a＜1时，不合题意．
所以，a的取值范围为[1，2）．
分析：先化简集合A，在根据条件（1）若A不属于B则，（2）若B⊆A，讨论a的取值范围．
点评：本题主要考查集合间的包含关系，较为简单，只需化简集合A，B计算可，注意分情况讨论．
练习册系列答案
相关题目
）y-3≥1，且y∈N*}，C={（x，y）|x∈A，y∈B}，D={1，2，3，4，5}，从C到D的对应f：（x，y）→x+y，则f是否是从C到D的映射？