题目内容
设△ABC的内角A、B、C所对的边分别为a,b,c,若simB+simC=2simA,3a=5c,则角B=( )
A. 60 B. 90
B. 90 C. 120
C. 120 D.150
D.150
C
解析试题分析:∵3a=5c,∴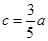 又∵simB+simC=2simA,根据正弦定理可得b+c=2a,所以b+
又∵simB+simC=2simA,根据正弦定理可得b+c=2a,所以b+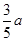 =2a,即
=2a,即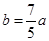 ,由余弦定理可得 cosB=
,由余弦定理可得 cosB=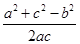 =
=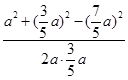 =
= ,所以B= 120
,所以B= 120 ,故选C.
,故选C.
考点:正弦定理和余弦定理

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
在 中,
中, ,则此三角形解的情况是( )
,则此三角形解的情况是( )
| A.一解 | B.两解 | C.一解或两解 | D.无解 |
在△ABC中,已知 ,则角A为( )
,则角A为( )
A. | B. | C. | D. 或 或 |
在 中,
中, ,
, ,
, ,则
,则 的面积为( ).
的面积为( ).
A. | B. | C. | D. |
在 中,角
中,角 的对边分别为
的对边分别为 ,若
,若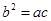 ,且
,且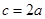 ,则
,则 等于( )
等于( )
A.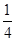 | B.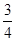 | C.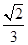 | D. |
已知点A(1,3), B(3,1 ), C(-1,0),则 的面积为( )
的面积为( )
| A.5 | B.6 | C.7 | D.8 |
在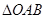 中,
中, ,
, ,
, ,则
,则 =( )
=( )
A. | B. | C. | D. |
 B.
B. C.
C. D.
D.
 中,角A、B、C所对的边分别为a,b,c且a=1,B=45°,
中,角A、B、C所对的边分别为a,b,c且a=1,B=45°, =2,则b 等于( )
=2,则b 等于( ) D.
D.